A fizikát, mint tantárgyat a gyerekek nem nagyon kedvelik. Ezt több felmérésen keresztül bebizonyították már. De vajon elgondolkodtunk már azon, hogy vajon miért van ez így? Persze, hogy igen és próbálunk is változtatni rajta. Mint tudjuk a fizikának nagyon fontos szerepe, van a természettudományos nevelésben. Ezért igyekeznünk kell valahogy érdekesebbé tenni a gyerekek számára.

Persze tudjuk, hogy mindenki azt teszi és igyekszünk a gyerekeknek megfelelő és érdekes feladatokat találni. De vajon hogyan jelenik meg a fizika a tankönyvekben? Erre a kérdésre próbálok meg válaszolni. Vagyis ezen belül a termodinamika milyen mélységben tárgyalja az új fogalmakat. Mennyire érthetőek az új fogalmak a gyerekek számára, ugyanakkor mennyire tudják elkülöníteni ezeket, a fogalmakat egymástól. Mindezt nem csak magyarországi tankönyvekben szeretném megvizsgálni, hanem szemügyre veszem a szerbiai és a lengyelországi tankönyveket is. Meg szeretném nézni, hogy mik a különbségek és hasonlóságok az országok tankönyvei között. A könyveket, melyeket kiválasztottam, mind nagyon jók és mindegyik népszerű tankönyvsorozatnak tekinthető. Ezekből a 7.-es és a 10.-es tankönyveket vizsgálom, mert ezeken, az évfolyamokon tanulnak hőtant.

Ami a legjobban érdekel, hogy a tankönyvekben hogyan jelenik meg az energia. Mert tapasztalatból tudjuk, hogy a gyerekek még mielőtt bármit is tanulnának az energiáról, már van egy tudásuk a mindennapi életből. Ez a tudás viszont nem egyezik meg azzal a tudással, amit a fizikaórán tanulunk. Ezt szeretném megnézni, hogy a tankönyvek mennyire figyelnek fel erre a kettőségre, mennyire próbálják meg elkülöníteni az energia két jelentését egymástól. Felhívják- e a figyelmet arra, hogy a kettő nem egy és ugyanaz?

De itt talán nem csak az energiával vannak gondok, csak valahogy ez tűnik a legsúlyosabbnak, hisz végigvonul az egész fizikán, és ha ezt nem értik meg rendesen a gyerekek, akkor talán az egész fizikát nehezen fogják. Az energia termodinamikában is jelen van, sőt ott ismét megjeleni egy újabb energiafajta, a belső energia. De nem csak az energia új, hanem sok más olyan fogalom is megjelenik, mely a gyerekek számára új. De ugyanakkor olyanok is megjelenek, melyek nem jelentenek újdonságot a gyerekeknek, és ezekkel mennyire foglalkoznak a tankönyvek? Meg szeretném nézni melyek ezek, mennyi van belőlük és mennyire érthetőek.

Persze az új fogalmakat mindig nehéz elsajátítani, de ha úgy magyarázzuk meg és írjuk le, hogy a gyerekekhez közel álljon akkor talán könnyebben, megjegyzik. Ezért szeretnék a dolgozatomban egy olyan bevezetését bemutatni az energiának, amely talán megkönnyítené a diákoknak annak megértését. Meg mutatni a hétköznapi és a fizikai energia közötti különbséget. A hétköznapi energiára egy új kifejezést kellene bevezetni az exergiát és ezt is részletesen bemutatni a gyerekeknek, hogy világosabb legyen számukra.

Sokszor egyes tantárgyak között is keveredik az energia, az erő vagy a munka fogalma. A gyerekek nehezen különítik el egymástól ezeket, a kifejezéseket. A tanulóknak bizonyos elképzeléseik vannak egyes dolgokkal kapcsolatban még mielőtt arról tanultak, volna az iskolában. Ugyan így az energiáról is vannak előzetes ismereteik, mégpedig, hogy az energia termelődik, vagy elhasználódik, tehát nem érvényes az energia megmaradás elve. A gyerek a mindennapi életben azzal találkozik, hogy az energia elfogy, hiszen fizetnünk kell érte, de ugyanakkor korlátlan mennyiségben áll rendelkezésünkre, hiszen mindig tudjuk pótolni. Az energia megmaradást tehát tanulnunk kell, ami viszont elég nehéz feladat, ahogy a tapasztalatok mutatják. (Radnóti) Erre szeretném felhívni a figyelmet, és ha lehet, akkor javítani rajta.

A fizika oktatása

A természettudományos képzés a közoktatásban az elmúlt időszakban a háttérbe szorult, a követelmények és az óraszámok is csökkentek. Sokszor arra hivatkoznak, hogy a gyerekekkel nem lehet semmit rendesen megtanítani, mert nincs rá elég idő. A fizikaórákon viszont legyen elég kísérlet, amivel a gyerekek gyakorolhatják tudásukat, és ha kell, akkor az anyag egyes részeit többször is át kell ismételni, hisz „ismétlés a tudás anya „.( Fizikai Szemle 2004/1 27.o.) Az ismétlés egyik módja, ha sorba kiemeljük a kulcsfontosságú kérdéseket, és ezeket mélyítjük el, de a leghatékonyabb, ha más sorrendben ismételünk, mint amilyen sorrendben tanultunk. (Vantsó, 2000)

A fizikatanítás az általános természettudományos műveltséghez való hozzájárulás, a fizikának több természettudományban, valamint a technikában ugyanakkor a minket körülvevő környezetben jelentős szerepe van. Ugyanakkor fel kell készíteni a tanulókat a tovább tanulásra, vagyis az új fizikai ismeretek befogadására.

A fizika a 7. évfolyamon jelenik meg, az előző évfolyamokon mármint 5. és 6. osztályban a Természettudományos ismeretek Fizika blokkjának célja a tárgy tanításának előkészítése. A 8. évfolyamon folytatódik a fizika tanítása tovább. A 9. évfolyam viszont már elég heterogén csoport, mások az ismeretszintjeik a gyerekeknek,a kifejezőkészségeik, tanulási gyakorlataik, és még lehetne sorolni a különbségeket, ezért ebben a tanévben talán érdemesebb kevesebb új ismeretet közölni és inkább az egyes tantárgyakra jellemző módszereket kell kialakítani. Ezért ez a felzárkóztatás a szintre hozás időszaka. A fizika szokásos fogalomrendszerének felépítése ezért inkább 10. és 11. évfolyamra kerül. ( Vantsó, 2000)

Mint ahogy az elején is említettem a fizikaoktatásra fordított óraszám jelentősen csökkent, és ebben a szűkösre szabott időben kell tanítanunk új anyagot, feladatmegoldást kísérletek bemutatása is be kell férjen. Ezek szerint el kell fogadni, hogy kevesebb óraszámban kell a fizikaismereteket átadni, mindazt az ismeretanyagot, amit eddig sokkal több órán keresztül taníthattunk. A fizika tantárgy iránti elvárás azonban nőtt. Az órákon egy korszerű természettudományos világképet kell kialakítani, és nem csupán átadni az elméletet és feladatokat megoldani. Tehát arra kell figyelnünk, hogy ne a feladatmegoldást fogadjuk el a fizikatudás fontos szintmérőjének. Ne csak száraz képleteket tanuljanak, hanem a képletek mögött fedezék fel az igazi jelentését is. A problémamegoldó gondolkodást próbáljuk meg kialakítani egy-egy fizikapélda megoldásánál, és ne csak kész sémákat alkalmazzunk, ahova behelyettesítünk, mert így nem fejlesztjük a tanuló képességeit. Tehát a száraz fizika mellett, egy gyakorlatiasabb életszagú fizikát kell tanítani, egy olyan fizikát, amely a gyerekekhez is közel áll, kapcsolatban van más tudományokkal is. Tehát egy modern természettudományos világképet kell kialakítani, hisz ennek alapja a fizika.

Már régóta folynak a kísérletek, hogy hogyan lehetne hatékonyan tanítani a természettudományokat köztük a fizikát, hogy azok számára is hasznos legyen, akik a mindennapi életben szeretnék alkalmazni tudásukat. Itt azokra gondolok, akik nem a felvételire készülnek. A nekik szánt természettudomány inkább érdekes kell, legyen, érdeklődés felkeltő, hogy aztán ezt a mindennapi életben is hasznosítani tudják.

A fizikát megfigyelésekből, tapasztalatokból, kísérletekből és mérési adatokból lehet megismerni. A fizikatanítás keretei között megfelelő tudományképet is ki kell alakítani. Itt arra kell törekedni, hogy modern tudományelméleti képet alakítsunk ki. Azonban megállapíthatjuk, hogy még a gimnáziumban sem szerepel kellőképpen a 20. századi fizika, tehát nem kapnak elég teret a modern ismeretanyagok. Kimaradnak a modern fizika olyan látványos területei, mint a kozmológia, vagy a nem egyensúlyi termodinamika jelenségei, a fraktálok stb. pedig lehet, hogy a hétköznapokban való eligazodás ezt követelné meg leginkább.

Ha megfigyeljük napjainkban a fizika túlságosan, koncentrál a feladat megoldásra. Persze ez talán érthető is, ha a gyerekeket az érettségire készítjük fel, de ugyanakkor figyelni kell arra is, hogy fejlesszük a problémamegoldó kézségeket, a kritikus gondolkodást, a jó fizikai világkép kialakulása vagyis, hogy meg tudják oldani a feladatokat de, ugyanakkor át is lássák a fizikát és használni tudják a mindennapi élet folyamán. (Vantsó, 2000)

A fizika megítélése

Mint tudjuk a fizika nem népszerű tantárgy a gyerekek körében. Egyik felmérés szerint nem a gyerekektől, hanem a tanároktól kérdezték meg, hogy véleményük szerint mennyire tartják fontosnak a gyerekek, és a szülök a fizika tantárgyat. A középiskolai fizikatanárok szerint a gyerekek: 2,64 + 0,71-re értékelik, míg az általánosban: 3,23 + 0,70. A felmérés szerint a középiskolában tanító tanárok szerint a szülők: 2,92 + 0,71 értékelték, míg az általános iskolai tanárok szerint: 3,28 + 0,73-ra. ( Radnóti)

Amint látjuk a tanárok szerint egyetlen gyerek sem tartja fontosnak a fizikát. A tantárgy megítélése drámaian romlik, talán ezért kellene a fizikának, mint tantárgynak jelentős megújuláson keresztül mennie. Ezért a tanároktól azt is megkérdezték, hogy mennyire elégedetek a fizikában tanítandó témakörökkel, melyiken kellene változtatni. De a tanárok nagy többsége nem válaszolt erre a kérdésre. Vajon mi lehet ennek az oka? Talán, mert már megszokták, hogy ezt kell tanítani, ők is ezt tanulták, és nem érzik azt, hogy bármit is változtatni kéne. Ugyanebből a felmérésből tudhatjuk meg, hogy a tanárok meg vannak elégedve a tankönyvválasztékkal. Viszont a taneszközökkel már nem annyira.

A tankönyvekben összeállított tananyag általában szükséges és elegendő, néha még kiegészítik őket munkafüzetekkel, vagy különböző taneszközökkel. A tankönyvek a lényeget általában kiemelik, vastag betűkkel vagy bekeretezik stb. Szemléltetik a tananyagot, de a tanulói aktivitásra nem nagyon figyelnek oda. Néhányon kívül ahol találkozunk olyan kísérletekkel melyeket a diák otthon is elvégezhet. De csoportunkára serkentő feladatokkal nem igazán lehet találkozni. Viszont képleteket begyakorló feladatok, vagy táblázatok azok elég nagy számban megtalálhatóak a tankönyvekben. Kevés a valódi problémahelyzetek megoldását követelő gyakorló feladat. Kevés az olyan szövegrész is, ami más területeken alkalmazott fizikát mutatná be. A tankönyvek tagolása arra készteti a tanárt, hogy frontális órákat tartson, és szinte egy - egy anyagrész egy – egy órának felel meg.

De ha megnézzük az újonnan megjelent tankönyvekben néhány kivételével, nem jelent meg újszerű pedagógiai szemlélet. Mindössze az anyag sorrendje változik a tantervi követelményekhez igazodva. A hétköznap életből vett tapasztalatok vagy a fizika szeretete ritkán jelenik meg a tankönyvekben, de ebbe most nem szeretnék mélyebben belemenni, majd a későbbiek folyamán lesz még erről bővebben szó.

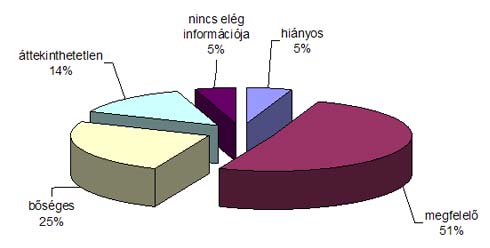
1.Ábra Fizikatanárok véleménye a tankönyv választékról.

Ha a fizikatanítás folyamatát figyeljük meg, mondhatjuk, hogy eléggé ódivatú. Abban gondolkodunk, hogy a gyerekek is „alulról felfelé haladva” ismerik meg a fizikai világot, holott a legmodernebb programok szerint a gyerekek aktívan építik magukba a körülöttük lévő világot. Tehát a gyerek nem tiszta lappal indul az iskolába, már előtte bizonyos meglévő tudással rendelkezik, és ebbe a már meglévő tudásába próbálja meg beilleszteni az újonnan tanult ismereteket. Ragaszkodnak eredeti elképzeléseikhez. Persze megtanulják az ami a tankönyvekben le van írva, csak nem biztos, hogy alkalmazni is tudják, hisz a valós világról teljesen mást gondolnak és mások a tapasztalataik. ( Radnóti 2002)

Energia probléma

Talán egyik nagyobb probléma a fizikában az energia, melyről teljesen mások a tapasztalataink, mint amit a fizikaórákon tanulunk. Viszont ennek megértése nagyon fontos lenne, hisz ez a fogalom végigkíséri az egész fizikát, és ha ezt nem értik kellőképpen a gyerekek, akkor lehet, hogy ez egész fizika nehézséget jelent számukra. A fizika tanítás problémái között persze nem az energia tehető az első helyre, de talán az egyik legfontosabb mennyiség, amit meg kell tanulnunk. Valamint az egyike azon mennyiségeknek melyekkel több helyen is találkozhatunk a mindennapi életben.

Mint tudjuk az energia a változásra való képességet, a fizikában a munkavégzőképességet jelöli, vagyis így ismerjük. A fizikában különböző energiaformákról szoktunk beszélni, az egyik legalapvetőbb a mozgási vagy kinetikus energia. Talán ez az energiaforma áll legközelebb a gyerekekhez is, hisz ezt használjuk legtöbbet a mindennapi életünk folyamán. Már tulajdonképpen akkor is erre gondolunk, ha azt mondjuk, hogy nincs energiánk futni, vagy ha egy kisgyerek jön - megy egésznap akkor azt is, mondjuk, hogy mennyi energiája van ennek a gyereknek. Lehet, hogy ilyen szóhasználatok miatt ragad meg a gyerekekben ez az energiaforma a legjobban. Azonban mint tudjuk a fizikában, megjelenik még a potenciális energia, gravitációs energia, elektromágneses energia és még sorolhatnám, de mégis mindig inkább a mozgási marad meg bennünk.

Ha megvizsgáljuk a tankönyveket, láthatjuk, hogy egyik helyen az energia, mint munkavégző képesség szerepel, de ugyanakkor tanuljuk, hogy az energia egy megmaradó mennyiség. De vajon tényleg megmarad-e? Ez a kérdés sokszor felmerül bennünk, hisz a hétköznapi tapasztalatokban nem ezt látjuk. A mindennapi életben sokszor azt haljuk, hogy az energia elfogy, vagy újratermelődik. Talán ezek okoznak gondot az energia megértésében, hisz sokszor a tankönyvek sem különítik el a hétköznapi energiát a tudományos, vagyis a fizikában tanult energiától. Ugyanis a gyermeki elképzelésben az energia „elfogy és újratermelődik”, tehát nem érvényes benne az energia megmaradás elve. Ezek szerint ezt meg kell tanulnunk, ami viszont nem könnyű feladat és sajnos a tankönyvek se segítenek minket ebben. Elég gyakoriak azok a példák, amelyek megerősítik a gyerekben azt a tudatot, hogy az energiát valóban előállítják.

Gondot okozhatnak pl. az energiának a mechanikai munkával történő bevezetése, itt a munka szó hétköznapi jelentése kavarhat be a gyerekeknek, és erősítheti az elképzelésüket is az energiával kapcsolatban. Itt a munka a test energiájának változásához kapcsolható inkább és nem a test energiájához. Inkább csak a mechanikai kölcsönhatások vizsgálatára alkalmazható. Zavart kelthet még a potenciális energia bevezetése, ez gyakran problémát okoz a gyerek számára, hogy mihez is kell rendelni a potenciális energiát. Különösen gond van akkor, ha a tankönyv vagy a tanár magyarázata nem következetes, hol ide, hol oda rendeli a potenciális energiát. De ez valahol érthető is, hisz 13-14 éves gyerekeknek a tankönyvszerzők még nem kívánják értelmezni az erőterek energiáját. (Radnóti 2002)

Tehát azt láthatjuk, hogy az energia bevezetése elég sok gonddal jár, különösen az energiamegmaradás, hiszen számolnunk kell a saját gyermeki elképzelésekkel, és az ezzel együtt járó tanítási nehézségekkel. Kisebb gyerekeknél az is elfordulhat, hogy az energiát kifejezetten élő szervezetekhez rendelik hozzá. Az energia a „tevékenységre való képességgel” azonosul, és az energia és az erő se nagyon különíthető el a kicsik fejében. De ha a kisiskolások könyveit megnézzük, ott is feltűnnek olyan hibák ahol az energiát, és az erőfogalmakat keverik. Ezekre a különbségekre viszont fel kell hívni a gyerekek figyelmét.

Energia fogalmak:

Hat különböző energia fogalmat különböztethetünk meg:

1) Saját működő képességünk. Ezt az energia fogalmat használjuk leginkább a hétköznapjainkban. „ Kimennék veletek este, de nincs elég energiám.”

3) Energiamegmaradás. Ez a fizikában jól definiált törvény. Feynmann egyik Nobel díjas fizikus ezt írja az energia megmaradásról: „létezik egy olyan energiának mondott mennyiség, amely változatlan marad a természetben folyó változások közepette. Ez igen absztrakt, elvont gondolat, egy matematikai elv:azt szögezi le, hogy van egy olyan számszerű mennyiség, amely nem változik bármi, történjék is.”

4) Munkavégző képesség: A mérnököknél ez egy jó definiált fogalom és ezt exergiának nevezik. Az exergia a hétköznapi energiának megfelelő mennyiség. „Az energiaforrásból bizonyos adott feltételek mellett maximálisan kinyerhető energiát exergiának nevezzük,” Fényes Imre Termodinamika és termosztatika című könyvében ezt a definíciót adja az exergiára.

5) Gazdasági energia: A biológiai rendszerek nem egyensúlyi rendszerek termodinamikai szempontból. A legfejlettebb rendszer van a legnagyobb távolságra az egyensúlytól. A biológiában és a gazdaságban az exergia azon része van figyelembe véve, amely felhasználható. Biológiai energia a napenergiából származik. A napból származó energia továbbítódik a növényekbe és az állatokba, mint kémiai energia az atomok közötti kötésben. Minden élő szervezet az emberiséget is beleértve energiát pocsékol. Néhány termelési folyamatban egy fontos tényező egyszerűen azonosítható: anyagok, pl. bizonyos kémiai vagy molekuláris összetevők, amelyek nem egyensúlyi rendszerek. Ezeket , az inputokat átalakítják. A létrehozás az exergia átalakítása egy kevésbé használható energiaforrásból egy jobban használható formába. Az energiahatár a gazdaságban nem egyszerűen az exergia használható része, de tartalmaz egy becslést is.

6) Pseudoenergia: Néha ezek a misztikus energiahívők valódi, tudomány által elismert energiaként tekintenek ezen energiákra. Számukra a középiskolás fizikaoktatás alapot nyújt ezen „misztikus” energiák megértéséhez (Newtoni energia fogalom).

Az energia egy képzeletbeli, absztrakt fogalom, amelyik azonban napjaink szókincsének sok részén mindennapivá vált, amit átitattunk konkrét létezéssel. ( Martinás )

Ezt a hat energia fajtát tudjuk megkülönböztetni, és arra kell vigyázni, hogy a gyerekek ne keverjék össze. De sajnos a tankönyvek nem segítenek abban, hogy ezeket el tudjuk határolni egymástól és egy pontosabb érthetőbb fizikai energiát, tanuljunk meg. De ezt most még nem részletezném, majd kitérek még erre a témára.

Ha megnézzük az energia szó jelentése- munkavégzőképesség, és ezt mondjuk az energia egyik fajtájának is. De ez nem, azaz energia, ami a mindennapi életben is használunk, és amiért fizetnünk kell, ez a fizikában elterjedt mennyiség, ami viszont nem a tényleges munkavégző képesség. A ténylegesen felhasználható energiára a mérnöki gyakorlatban használt exergia elnevezés a pontos. A fizikai energiát belső energiának hívjuk, és ennek megmaradása azt jelenti, hogy nem létezik első fajú perpetuum mobile, vagyis nincs olyan gép, amivel a semmiből munkát tudnánk előállítani. Az energiamegmaradás a fizika egyik legfontosabb törvénye, mindent összemérhetővé tesz.

Az energiának, mint említettük több jelentése van, és ez az egyik leggyakrabban használt szavunk. Az energia kapcsán gyakran találkozunk a következő kifejezésekkel:

Az energia megmarad

Az energia elfogy

Az energia termelhető

Most feltehetjük a kérdést, hogy vajon melyik igaz? Ha jól belegondolunk akkor mindhárom kijelentésünk igaz, csak akkor más-más energia fogalmat értünk alatta.

Tankönyvek felépítése

A termodinamika hatásfoka kicsi, és erre próbálom megkeresni a választ, hogy mi ennek az oka. Három különböző országból választottam ki néhány tankönyvet és ezeket hasonlítom össze, hogy megnézzem melyek a különbségek és hasonlóságok közöttük, elsődleges cél az volt, hogy egyes országokban mennyire reflektálnak a gyermeki energia és a fizikai energia különbözőségére. Megvizsgáltam néhány magyarországi, néhány szerbiai és néhány lengyel tankönyvet. A lengyel tankönyvek vizsgálatában Marek Frankowicz tanár úr és, Iwona Maciejowska tanárnő segítettek.

A tananyag nagyon sok, főleg termodinamikából, ha megvizsgáljuk, hogy hány órája van egy hetedikes diáknak fizikából évente akkor a tankönyvek alapján nagyon sok az anyag és ezt nem elég, hogy csak valahogy elmondják a fizikaórán, hanem a diáknak meg is kell értenie az összefüggéseket. Azt is megnézhetjük, hogy hány oldalas egy-egy ilyen tankönyv és hogy ebből mennyi termodinamika, hát elég sok.

Tankönyv	Oldalszám	A termodinamikai rész
Gulyás	143	38
Zátonyi	195	75
Csákány	155	51
Milan	121	25
Jovan	108	10
Karácsonyi	239	85
Pászli	211	70
Danilovic	197	96

2.Ábra

A táblázatból is lehet látni, hogy a tankönyvekben elég sok a termodinamikai rész. Mivel soknak tűnt és elég sok új fogalommal találkozunk a hőtani tanulmányaink során, ezért úgy döntöttem megszámolom vajon mennyi új fogalmat kell megtanulniuk a diákoknak tanulmányaik folyamán termodinamikából. Ezt is jobban összetudjuk hasonlítani, ha egy táblázatban nézzük meg a fogalmak számát. Azt, hogy melyek azok a fogalmak melyeket újnak gondoltam azok a függelékben megtalálhatóak. Az új fogalmakat a szerint válogattam, hogy mikor jelent meg először a tankönyvben és mikor lett először definiálva. Csak a termodinamikai részt vizsgáltam.

Primary/

Lower secondary

Csákány 58

Zátonyi 48

Gulyás 45

Milan 33

Jovan 37

38 (lower secondary)

Secondary

Pászli 59

Karácsonyi 32

Raspopovic 28

35 (upper secondary);

16 of them new

3. Ábra

A táblázatból kiszűrhetjük, hogy a Magyarországi tankönyvekben található a legtöbb

új fogalom, amit a gyerekeknek meg kell tanulniuk hetedik osztályban termodinamikából. A Szerb és a Lengyel tankönyvek körülbelül ugyan azon szám körül szóródnak. Igen most azt mondhatjuk, hogy akkor mivel Magyarországon a diákok többet tanulnak akkor többet is tudnak. Persze én itt nem ítélkezni szeretnék és persze ez nem muszáj, hogy azt jelentse, de mondjuk ha kevesebb dolgot tanítanánk meg a gyerekekkel lehet, hogy hatékonyabban és jobban megtanulnák azokat a fogalmakat is amelyek most nehézséget okoznak nekik.

Amint láthatjuk egyes könyvekben majd 60 új fogalmat, kell elsajátítaniuk. Lehet, hogy egy kicsit sok, ha megnézzük, hogy a gyerekeknek hány órájuk van összesen az évben, és ezeken az órákon nem mindegyiken termodinamikát tanulnak, hanem még mást is. Ha megnézzük az új fogalmak gyakran nincsenek rendesen definiálva, csak említés szintjén kerülnek bele a tankönyvekbe, mert feltételezik, hogy egyes fogalmak már elég jól ismertek a hétköznapi tapasztalatokból.

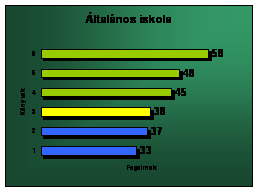
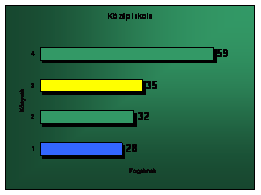
4. Ábra

A grafikonon az előző táblázat adatait ábrázoltam, hogy jobban össze tudjuk hasonlítani a könyvekben, szereplő szavak számát. Kék színnel jelöltem a szerbiai könyveket, zölddel a magyarországi tankönyveket és sárgával a lengyelországi könyveket. Úgy tűnik a Lengyel tankönyvek tartalmaznak termodinamikából a legkevesebb új fogalmat. A szerbiai könyvek is jóval kevesebb új fogalmakat vezetnek be a termodinamikában, mint a magyarországi tankönyvek. Az egyik ilyen fogalom, amit már az elején is említettem az energia, amit már a mechanikai részben bevezetnek, vagy például a teljesítményt, a hatásfokot a szerbiai tankönyv írok a mechanikai, részben vezetik be, míg ezekben, a magyarországi könyvekben a termodinamikai részben szerepel. De hogy melyik fogalom hol szerepel azt megtekinthető a függelékben.

Hasonlóságok és különbségek a tankönyvek között

A magyarországi tankönyvekben az energiát a termodinamikai részben vezetik be, míg a szerbiai tankönyvekben már a mechanikában megjelenik az energia fogalma. A tankönyvek termodinamikai részét hasonlítottam össze, hisz ott is szükség van az energia fogalmára pl. a főtételeken belül. De ugyanakkor nem csak az energia, hanem sok más új fogalom is megjelenik a termodinamikán belül, amit már a hétköznapi életünk folyamán tapasztalunk még mielőtt bármit is tanulnánk róluk fizika órán. Azt próbáltam megnézni, hogy ezekre az új fogalmakra mekkora hangsúlyt fektetnek a tankönyvírók, és mennyire érthetően írják le a fogalmak magyarázatát.

Arra a következtetésre jutottam:

Tulajdonképpen mindegyik könyv egyforma, kivéve talán az egyik szerbiai könyvet mely atomfizikával kezdi a termodinamika bevezetését (Raspopovic, 1997), a többi könyvnek a felépítése hasonló.

Egyik könyv se vesz példát a hétköznapi életből. Bemutatnak néhány kísérletet, melyet már a tapasztalatainkból tudunk, de olyan kézzelfogható példák nincsenek, melyek felhívnák a gyerekek figyelmét, hogy ekkor ezt most hol is figyelhetnénk meg a mindennapi életben.

A hőmérsékletet és a hőt ismertnek tételezi fel. Ugyan úgy, mint a belső energiát is.

A hőt a belső energiával vezeti be, a belső energiát pedig a hővel magyarázzák. Tehát nincs elkülönítve a kettő egymástól, és így tulajdonképpen az egyiket se magyarázza meg rendesen.

Valahogy nem lehet érezni, hogy a fogalmakat elkülöníti egymástól és egy kialakult érthető képet, alakítanának ki az a gyerekek fejében.

Persze a tankönyvek önmagukba véve jók, de mégis mintha egy kis zavart okoznának a gyerekekben, mert ha nem különíti el a fogalmakat egy mástól és az egyik új fogalmat egy másik, olyan fogalommal definiálja, ami még nem teljesen tiszta, akkor így a gyerekeknek is nehezebb lesz megtanulni az adott anyagot.

A másik nagyobb probléma, hogy a tankönyvek az energiára se fektetnek túl sok hangsúlyt. Nem különítik el a hétköznapi energiát a fizikában tanult energiától. Nem mondanak példákat arra, hogy mi a kettő között a különbség. Nem hívják fel a figyelmet arra, hogy az energiamegmaradás, hogyan is jelenik meg a mindennapi életben. Amire viszont szükség lenne, hogy a gyerekek megértség az energia megmaradást, hiszen ezt nem igazán tapasztaljuk a mindennapi életünk során.

Szóval, amire fel szeretném hívni a figyelmet, hogy a tankönyvek sok új fogalmat ismertnek tételeznek fel, ami talán nem is olyan triviális a gyerekek számára. Valamint egyes fogalmakat nem különítik el egymástól. De a dolgozatomban még minden egyes problémára kitérek részletesebben.

Energiamegmaradás

Az energiamegmaradás törvénye szerint, a zárt rendszer energiája megmarad, az egyes összetevők energiája nem változik. Ez a tétel, mint már fentebb is említettem három ember nevéhez fűződik, akik egymástól függetlenül fedezték fel ezt a törvényszerűséget. De a mindennapi életben tényleg ezt tapasztaljuk? Ezt már többször is említettem, hogy nem és ez a legnehezebb a gyerekek számára. Ezért kellene ennek a megtanítására kicsit több időt fordítani az iskolában a tanároknak és a tankönyvíróknak ugyan úgy. Hisz az energia maga már egy elég absztrakt fogalom a fizikában, amit el kell különítenünk a hétköznapjainkban használt energiától, és erre szeretnék kitérni és megvizsgálni, hogy a tankönyvek, hogyan magyarázzák az energia fogalmát. Hogyan lehetne, hatékonyabbá és érthetőbbé tenni az energia bevezetését a középiskolában. E célból több tankönyvet vizsgáltam és elemeztem, hogy talán könnyebb lesz megtalálni a választ a nehézségekre. A tankönyvek termodinamikai részét tanulmányoztam részletesebben, mert talán az is egy elég kemény anyag lehet a gyerekek számára és ott is megjelenik az energia fogalma. A tankönyvek összehasonlítását nem csak Magyarországon belül végeztem, hanem Szerbiában és Lengyelországban is. Remélhetőleg a dolgozatom végére kiderül melyik országban hatékonyabb a fizika, és ezen belül a termodinamika tanítása.

Energia a tankönyvekben

A fizikatanítást általában a mechanikával kezdik a tankönyvek. A mechanikán keresztül vezetik be az energiát. Ennek csak az a veszélye, hogy a gyerekek nehezebben különböztetik meg a fizikai energiát a hétköznapi energia fogalomtól. Itt nem azt akarom mondani, hogy a tankönyvírók nem ismerik az energia fogalmat, hanem inkább arra, mint amit az elején is említettem, hogy a gyerekeknek már kialakult egy kép e fogalomról és ezt talán nehezebb tisztázni a mechanikában bevezetett energiával, ahol először a munka fogalmát kell megtanítanunk a gyerekkel. Majd ezek után vezetjük be az energiát, és egyes tankönyvek azt mondják, hogy az energia munkavégzésre való képesség. Ami viszont a hétköznapi energia (exergia ) és nem az energia, amit fizikainak nevezhetünk.

Más tankönyvek az energiát példák alapján vezetik be. Az egyik ilyen tankönyvből vett példa, ahol azt írja, hogy ha egy álló kocsinak nekiütközik egy másik, akkor az első a másik mozgó kocsi hatására indul el. Ezzel magyarázza, hogy egy test képes más test sebességét növelni, és e testeknek energiájuk van. Majd külön ugyan így példákon megmagyarázza a különböző energia fajtákat is.

A Magyarországi hetedikes tankönyvekben, nem nagyon fordul elő, hogy a mozgási energiát vagy bármely energiafajtát külön képletekkel is definiáljanak, míg az egyik szerbiai tankönyvben találhatunk már képleteket és számolási feladatokat is. Persze itt sincsenek levezetve a képletek, csak a végleges van feltüntetve és ehhez a legegyszerűbb feladatok és megoldásaik. Mielőtt közölnék a jól ismert, képletet, előtte kíséretekkel elmagyarázza, melyik testnek nagyobb az energiája. Ha két különböző tömegű testet egy lejtőről leengedünk és ugyanakkora sebességet érnek el a lejtő alján, akkor annak lesz nagyobb az energiája, amelynek nagyobb a tömege. Ezt úgy tudták megállapítani, hogy a lejtő aljához egy hengert helyeztek, és azt tapasztaljuk, hogy a legnagyobb tömegű golyó löki legmesszebbre a hengert. Ezek után azt is megvizsgálják, hogy ha ugyanazon golyót a lejtő különböző pontjából indítunk el akkor viszont az löki messzebbre a lejtő alján elhelyezett hengert amelyiket a lejtő legmagasabb pontjából engedtünk el. Majd ugyan így a potenciális energiát is bevezeti, vagyis ehhez hasonló módon.

Itt most a kinetikus és potenciális energiára, hoztam fel egy pár példát, csak hogy láthassuk a különbségeket a magyarországi és a szerbiai tankönyvek között. Ezt az energiát a mechanikai részben tárgyalja. Míg a magyarországi hetedikes tankönyvek melyeket kielemeztem inkább a termodinamikai, részben foglakoznak az energiával. De ugyan úgy mechanikai útón megközelítve a fogalmat. Egyik ilyen tankönyvben először a belső energiáról beszél és csak utólag az úgynevezett mechanikai energiákról. De a termodinamikai részre inkább később térnék ki.

Visszatérve a mechanikai energia fogalomhoz, melyhez egy munkavégző képesség kapcsolódik és nem egy megmaradó mennyiség, talán ez lehet a probléma oka. Mert a mechanikában bevezetett energia megfelel a hétköznapi fogalmunknak, ami viszont nem marad meg. A tévében, a rádióban mindenfelé azt haljuk, hogy energia válság van, ami viszont csak arra utal, hogy az energia nem marad meg. Tulajdonképpen ezt tényleg nem nagyon tapasztaljuk a mindennapi életünk folyamán, hogy megmaradna. Mert ha megmarad akkor mi miért kell fizessük a fogyasztásunkért, hiszen nem használunk el semmit, mert azt mondtuk, hogy megmarad. Mondhatnák a gyerekek. A mechanikai energiamegmaradással talán nincs is akkora gondjuk, mint a termodinamikaival. Hiszen a mechanikai energiamegmaradás csak speciális estekben érvényes.

Termodinamika a tankönyvekben:

Az elején már egy kis átfogó bevezetőt adtam a tankönyvekről, most azonban egy kicsit részletesebben is megvizsgálnám a tankönyvek összetételét, azon belül is a termodinamikai rész. A tankönyvek általában sorozatokban jelennek meg, én nem egy egész sorozatot szeretnék itt szemléltetni, csak egy bizonyos korosztálynak szóló tankönyvet ezek között is a hetedikes és a tizedikes tankönyveket, mert a termodinamikai részt szeretném részletesebben kifejteni.

Az egyik könyv a Károlyházy - Csákányné címmel ismeretes, használják az egész országban, az ábrái nem annyira színesek, de humorosak és igényes magyarázószövegei vannak. A másik tankönyvcsalád a Zátonyi Sándor nevéhez fémjelezhető, ez a tankönyvsorozat a fizikaoktatás teljes időtartamát lefedi. Népszerű a középiskolákban használt humán érdeklődésű diákok számára készült Karácsonyi sorozat. Ugyanakkor népszerű még az emelt szintű fizikaoktatást támogató tankönyvsorozat melyet a Radnóti Gimnázium tanárai állítottak össze.

Ha fizikai tankönyveket veszünk a kezünkbe, azt gondolnánk, hogy a fizika tanítása nem tekintélyelveken, hanem természeti megfigyeléseken, kísérleti alapokon nyugvó tudomány. De a tankönyvekben nem ezzel találkozunk. Lehet furcsán, hangzik, de a klasszikus fizika az amiről a legkevesebbet tudunk. Elég sok kérdés merül fel bennünk, hogyan is kell értelmezni az energia vagy az impulzus fogalmát? Mit is jelent az idő, az erő, vagy az erőtér fogalma? Ezek azok a fogalmak melyeket nagy ívben kerülnek nem csak az általános iskolás, és a középiskolás tankönyvek, hanem még az egyetemi szakkönyvek is. Tehát a legalapvetőbb fogalmak eléggé ködösek és nehezen interpretálhatóak. Ilyenek a klasszikus fizika és az elektrodinamika, az egyetemi tankönyvekben, mert kísérleti eredményeket sehol sem lehet találni. Még ha érdekelné is a diákot nincsenek feltüntetve, hogy hol lehetne utána nézni. ( Egely, 2002)

Legrosszabb a helyzet a legátfogóbb törvényekkel, ilyen az impulzus és az energiamegmaradás törvénye. Tudjuk, hogy ezek érvényesek a fizikában és a biológiában is egyaránt. Mint már említettem az energiamaegmaradás végigvonul az egész fizikán, ezért fontos, hogy a gyerekek megértsék, ami viszont elég nehéz, mert nem tudunk kísérleti bizonyítékokat mutatni, és a mindennapi életben sem ezt tapasztaljuk. A termodinamikai ismereteinkben kétségtelenül érvényes az energiamegmaradás.

A hőtan jelenségek anyagszerkezeti magyarázata már az 50-es és 60-as években megjelent a tankönyvekben, de teljes polgárjogot, csak az 1978-as tantervben nyert. Napjainkban pedig már elképzelhetetlen lenne a fizika tanítása a hőtani jelenségek korpuszkuláris magyarázata nélkül.

A tankönyvekben koncentrikusan épülnek ki a hőtani alapfogalmak. Az általános iskola alsós kisdiákjai még csak megfigyeléseket végeznek, különböző anyagokat vizsgálnak és csoportosítanak halmazállapotuk szerint. A vizet, egy picit mélyrehatóbban vizsgálják meg, megnézik annak halmazállapot változásait. Alapvető ismereteket szereznek a hőmérséklet fogalmáról, valamint az energiáról. ( Radnóti 2002)

Az 5-6. osztályban a természetismeret keretein belül megismerkednek a részecskeképpel, a halmazállapot változásokkal, és a hő terjedésével majd a hő tágulások kvalitatív értelmezésével. Megjelenik a termikus kölcsönhatás fogalma, és az energia fogalmának tovább fejlesztése. Tananyagként megjelenik a termodinamika első fő tétele, ténylegesen még nem kimondva, csak a munka és a hő keretein belül.

A 7-8. évfolyamon kezdődik el a kvantitatív leírás. Itt megjelenik a fajhő, olvadáshő, forráshő, égéshőfogalmak, és még más egyéb új fogalom, melyekre a későbbiek folyamán részletesebben is kitérek. A felsőbb évfolyamokon tovább bővülnek az ismeretek. Itt már megjelenik az ideális gáz, mint kvantitatív modell, és ehhez már számolási feladatok is tartoznak szép számmal.

Kicsit részletesebben is kitérnék a tankönyvek vizsgálatára, vagyis a termodinamika megjelenésére a tankönyvekben. Azt szeretném megvizsgálni, mennyire pontosan vannak megfogalmazva egyes új fogalmak a tankönyvekben, különös figyelmet szentelve az energia fogalmom megjelenésének. ( Radnóti 2002)

A vizsgálataim az általános iskola 7. osztályos tankönyveire valamint a 10. osztályosokra terjed ki. Mivel napjainkban a diákok ezeken, az évfolyamokon tanulnak termodinamikát. Több tankönyvet elemeztem, Magyarországon megjelent tankönyvek közül, melyeket úgy próbáltam meg kiválogatni, hogy legyenek benne olyanok melyek magasabb szintű fizika tudást követelnek meg, és olyanok melyek egy kicsit egyszerűbbek. Majd ezeket hasonlítottam össze a szerbiai tankönyvekkel, valamint a lengyel tankönyvekkel.

Nézzük először a 7-.es könyveket. Mindegyik tankönyv a hőmérséklet bevezetésével kezdi el a hőtan tárgyalását. Vagyis inkább a hőmérséklet, mint ismert mennyiség bemutatása az első lépés. A hőmérséklettel empirikus módon, kísérletekkel ismerkednek meg a gyerekek Majd ezt követi a termikus kölcsönhatás, hőtágulás, hőterjedés, a fajhő az anyag részecskeszerkezete, majd a párolgás, olvadás, fagyás ezek után jelenik meg az energia, a hőerőgépek, a teljesítmény és a hatásfok. ( Zátonyi 2006 ) Ezek azok az anyagrészek melyek a magyarországi tankönyvekben megjelennek. Tehát ha megnézzük mindegyik a fenomenológikus bevezetést követi. Kivéve egy szerb tankönyvet mely a hőtant az atomfizikával vezeti be, és ezt követően jelenik meg a belső energia, hőmérséklet és a hőmennyiség. A tananyag többi része nagyon hasonló a magyarországi tankönyvekhez, azzal a különbséggel, hogy a hatásfokot nem a hőtan keretein belül tárgyalja, hanem a mechanikai fejezetben. ( Raspopovic 1997 )

A tankönyvek feltételezik, hogy a hőmérséklet és a hő jól ismert mennyiségek. A hőt a belső energia átadással definiálják. Nem igazán érzékelhető a különbség a hőmérséklet és a hő között. Különben is elég nehéz elkülöníteni ezt a két fogalmat egymástól, de ha még nem igazán hangsúlyozzuk ki a különbségeket, akkor a gyerekek nagy többsége azonosnak gondolja a két fogalom jelentését. Tulajdonképpen nem könnyű feladat e két dolog elkülönítése a gyerekek fejében, hisz ők mielőtt bármi kísérletet elvégeznének, először összegyűjtik az előzetes tudásukat, tapasztalataikat és gondolat kísérletet elemeznek.

A gyerekek eddig összeadódó mennyiségekkel találkoztak, vagy így alakult ki bennük, és most ha megjelenik a hőmérséklet akkor lehet, hogy nehezen tudják felfogni, hogy azt csak úgy egyszerűen nem adhatjuk össze. Hanem a termodinamika második főtétele alapján, a hőmérsékletek kiegyenlítődnek. Erre kell felhívnunk a diákok figyelmét. Továbbá a halmazállapot – változások során is arra gondolnak, hogy megváltozik, azaz növekszik a hőmérséklet értéke. Ugyanakkor a hőmérséklet egyensúly fogalma sem elég tiszta a diákok fejében. De ennek kialakítását elősegítheti a hőmérséklet mérése. Különböző hőmérsékleteket mérhetünk, mint ahogy az a tankönyvekben is fel van tüntetve, összehasonlíthatjuk őket. Például az egyik tankönyvben azt mérték le, hogy hogyan változik a víz hőmérséklete, miután kivették a hűtőből. A víz hőmérséklete kétpercenként lemérhető, és táblázatba feltüntethető akkor a gyerekek is láthatják a változásokat egy bizonyos idő elteltével. Itt észrevehető, hogy hogyan változik a hőmérséklet, és hogy valami történik közben, vagyis, hogy hőt ad le. Csak ez így nincs kihangsúlyozva a könyvben, pedig kellene, mert amint már említettem a gyerekek gyakran összekeverik a hő és a hőmérséklet fogalmát.

Ugyan úgy az energia bevezetése se könnyű feladat a tanár számára. A tankönyvekben több fajta energia is szerepel, a diákok már a mechanikai tanulmányaik során megtanulják a kinetikus, a potenciális a rugalmas energiát, majd az energiamegmaradás törvényét, ami viszont elég elvont a számukra. Majd a termodinamikában megjelenik a belső energia fogalma, ami szintén bonyodalmat okozhat úgy a tanárnak, mint a diákoknak. Itt már eleve gondot jelent, hogy mi is számít belsőnek. Egyes tankönyvek a belső energiát valahogy a hőmérsékletváltozással próbálják megmagyarázni., pl „ A testeknek azt az energiáját, amely melegítéssel, vagy hűtéssel megváltoztatható, belső energiának nevezzük.”( Gulyás fizika 7, 114 o.) Míg más tankönyvek a test részecskéinek mozgásából származó energia és a kölcsönhatásukból származó potenciális energia összegét nevezi belső energiának. ( pl 7. Raspopovic)

Alonso (1997) egyik cikkében, ezt írja fel: A rendszer energiája = a részecskék mozgási energiája + a részecskék kölcsönhatási energiája + a részecskék energiája

Tehát

E= E ( mozgási) + E ( kölcsönhatási) + E( részecske)

Ha ezt megvizsgáljuk az első taggal talán még nincs is gond, a részecske mozog. A második kölcsönhatási energia, ha az atomok között kötések alakulnak ki, de ekkor a rendszer energiát bocsát ki, tehát ez nem igazán tekinthető a rendszer energiájának alkotórészeként. A harmadik viszont talán egy anyagi rendszer energiája teljes egészében, mivel a mozgási energiáját már az első tartalmazza. ( Radnóti 2002)

A belső energia bevezetésével is nehézségekbe ütközünk. A belső energia nehezen megfogható és értelmezhető fogalom. Azt mondjuk, ha valamilyen kölcsönhatás vagy változás történik, akkor van egy mennyiség amely nem változik, csak átadódik, ezt sokszor hangsúlyozzák a tankönyvek is. De ha nincs kölcsönhatás a dolgoknak akkor is van energiájuk. Itt tekintsünk el mindenféle potenciális, vagy elektromos és más energiáktól. Minden anyaghoz tartozik egy belső energia, mely a hőmérséklettel arányos:

U=c m T

Tehát mind látható is arányos a hőmérséklettel, a tömeggel és az anyagra jellemző állandóval, ami a fajhő.

Ugyanakkor a középiskolás könyvek viszont, csak hivatkoznak arra, hogy ezeket már az általános iskolában megtanulták a gyerekek, mármint a hőmérséklet, hő vagy egyes könyvek talán még egyszer definiálják. A középiskolás tankönyvekben megjelenik az ideális gáz fogalma is, azonban erre ügyelni kell, hogy hogyan használjuk és, hogy felhívjuk a gyerekek figyelmét arra, hogy ez csak egy modell, és hogy a mindennapi életben ilyen nem igazán alkalmazható, ez talán csak a számpéldákban jó alkalmazható. Ezért vajon ha megnézzük érdemes ezzel kínozni a „szegény diákokat”? Ideális gáz a természetben nincs. De mint már az elején is említettem a diákok egy bizonyos tudással rendelkeznek, hisz tapasztalatokat szereznek az életben, amit aztán megpróbálnak a fizikai tanulmányaikba illeszteni. Vagy legalább is a saját elképzelésük szerint értelmezni a fogalmakat. Vajon ezt mennyire könnyen tudják elképzelni? Persze megmutatjuk a golyó modellt, mert az ideális gáz „molekuláit kiterjedés nélküli tömegpontnak tekintjük”. De vigyázni kell, nehogy a tanulókban az alakuljon ki, hogy a termodinamika nem is szól másról, csak az ideális gázról. Tudatosítani kell bennük, hogy ez csak egy modell.

A másik nagyobb probléma a termodinamikában a főtételek bevezetése, valamint az ehhez kapcsolódó zárt rendszerek és az energia. Hogyan is képzelhet el a gyerek egy zárt rendszert? John Ogborn egyik cikkében olvastam az erre nagyon jó választ. Ugye már kicsi gyerekként megtanuljuk, vagyis tapasztaljuk, hogy nem sétálhatunk át a szoba falán. Ezért egy zárt rendszert jól szemléltető kép lehet egy lezárt szoba. Ugye oda se be se ki nem tudunk közlekedni. Ilyen elképzelhető lezárt szobának korlátai vannak, megvan mi az ami megtörténhet és mi nem, pl. az energia mennyisége nem változhat. Semmi létező nem tudja elhagyni a szobát, így az energia sem szivároghat ki onnan, csak áramolhat az egyik sarokból a másikba. Semmi sem történhet, ha a lezárt szoba tartalma egyensúlyban van.

A hő és a hőmérséklet a tankönyvekben

A termodinamikát a tankönyvek először a hőmérséklet bevezetésével kezdik. Vagyis inkább egy ismertetést közölnek olyan kísérleteken keresztül, amit már a tapasztalataikból megtanultak a gyerekek. Mintha feltételeznék, hogy a hőmérséklet és ezzel együtt a hő is nagyon jól ismert fogalom a gyerekek részére és ezt nem kell külön definiálni. Sokszor viszont a hő és a hőmérséklet fogalmát se különböztetik meg. Ez viszont elég sok bonyodalmat okozhat a gyerekek további tanulmányaiban. Egyes könyvekben az áll, hogy a hőmérsékletet kezünkkel érezzük és ezzel még pontos adatokat, nem tudunk mondani, csak akkor, ha a hőmérőről leolvassuk a pontos adatot. Szóval a hőmérsékletet kísérletekkel, tapasztalati útón vezetik be a tankönyvek.

A hőt az általános iskolás könyvek átadott energiának, vagy energiaváltozásnak nevezik „Hőnek vagy hőmennyiségnek nevezzük a termikus kölcsönhatás közben átadott energiát.”(Csákány 2006 113. o.) Míg a középiskolás könyvek vagy hivatkoznak arra, hogy ezt már megtanulták az általános iskolában, vagy azok is hasonlóan definiálják a hő fogalmát: „A hő egy test (belső) energiája megváltoztatásának egyik lehetséges módja. Maga a hő tehát egy energiaváltoztatási út.” (.Karácsonyi 2003 53. o.)

Tehát mint látjuk a hőre, találunk definíciókat, míg a hőmérsékletre ilyen konkrét definíciót nem adnak a tankönyvek. Itt nem kritizálni akarom a tankönyveket, mert mindegyik jó és érdekes a maga módján, és biztos nem is olyan egyszerű egy ilyen tankönyvet megírni, sőt biztos vagyok benne, hogy nagyon sok munkával jár. Csak lehet, hogy mivel olyan sok az anyag ezért valahogy be kell osztani, hogy mire fektetnek nagyobb hangsúlyt és mire nem. De lehet, hogy pont azokon az alapfogalmakon csúsznak el, amelyeket érdemes lenne tisztázni, mert erre alapozzák a későbbi tudást. Lehet, hogy tényleg triviálisnak tűnik, és mindenki tudja, hogy mi a hőmérséklet, de talán a hő már kevésbé ismert.

Sokszor tényleg abban a hitben élünk, hogy vannak alap dolgok melyeket, megtapasztalunk, és talán tudjuk is. Ezért ezekkel nem kell annyit foglalkozni. Mindenki tudja, hogyha valamit melegítünk, akkor annak megváltozik a térfogata. Már biztos minden gyerek kipróbált valami szilárd testet melegíteni és tudja, hogy akkor annak térfogata megnő, ha hűtjük, akkor pedig összehúzódik. Tehát ezt is tudjuk tapasztalatból, de azért fizika órán erre is külön kitérünk, és kísérleteket végzünk, hogy a gyerekek minél jobban megértsék. Ha körbenézünk a környezetünkben, mindenhol ott van körülöttünk a fizika, és minden olyan triviálisnak és egyszerűnek tűnik. Akkor miért van, hogy fizikaórán mindenki újnak és ismeretlennek titulálja az anyagot? Talán, azért mert akkor azt gondoljuk, hogy az amit ott órán tanulunk az csak is bonyolult lehet. Pedig ha leegyszerűsítjük a dolgokat és a hétköznapi tapasztalatok alapján, magyarázzuk meg őket akkor érthetőbbé válnak, és közelebb kerülnek a diákokhoz.

Tehát a gyerekek sokszor már attól a szótól megijednek, hogy fizika. Gyakran olyan egyszerű kérdésekre nem tudnak válaszolni, amire nem fizikaórán könnyen tudnák a választ. Ilyen egyik példa, a sárosdi Farkas Gyula emlékére rendezett fizikaversenyen a gyerekeknek meg kellett magyarázni a jelenséget: ha a hőmérőt beletesszük forró vízbe, akkor a higany előbb lesüllyed és utána emelkedik. Voltak, akik megadták a helyes választ, de azért nagyobb részük nem tudta pontosan megmagyarázni, hogy mi is történik akkor. Voltak olyanok is akik gondolkoztak és hétköznapi tapasztalataik alapján próbálták megmagyarázni a jelenséget. Persze nem teljesen helyesen, de próbálkoztak. Az ő megoldásuk, úgy szólt, hogy ha mi is belenyúlunk a forró vízbe, akkor először hidegnek érezzük azt és csak utána melegnek. Valamilyen szinten igazat mondtak és látszott, hogy gondolkoznak, de itt nem ez volt a válasz és itt ők a hőáramról beszéltek. Voltak olyanok is akik az endoterm és exoterm hatással magyarázták a jelenséget: „ Ha a hőmérőt forró vízbe mártjuk, illetve sokáig bent tartjuk, akkor a higanytól hőt nyel el, amit endoterm hatásnak nevezünk. Kicsit lemegy a higanyszál és utána hirtelen meg fog emelkedni. Ennek oka, hogy a forró víz hőt ad át a higanynak, amit exoterm hatásnak nevezünk.” Csak egy részét idéztem annak, amit a gyerekek leírtak a versenyen. A megfogalmazás, jó csak sajnos a válasz nem. A helyes válasz az lett volna, hogy először az üveg tágul ki és ezért esik le a higany szintje, és utána mikor átveszi a hőmérsékletet akkor kezd emelkedni. Itt is látszott, hogy egyesek gondolkodnak és megpróbálnak a tapasztalataikra hagyatkozni, míg mások olyan fizikai kifejezéseket kerestek, melyek jól hangzanak. Sokszor nagyon egyszerű dolgokat is túlbonyolítunk fizikaórán, másokat viszont feltételezik, hogy már tudják a diákok, és nem nagyon foglalkoznak velük.

Itt megkérdőjelezhetjük, hogy megtanulták-e vagy tudják–e a hőtágulást. Ezek a gyerekek hetedikesek és nyolcadikosok, a hőtágulást hetedikben tanulják, persze még minden képlet nélkül, kísérletekkel és példákkal próbálják megmagyarázni a jelenséget. A hőtágulási együtthatót egy hetedikes fizika könyvben találtam meg.(Gulyás 2003) Hőtágulás részletesebb magyarázatára a középiskolában kerül sor. Itt már megjelenek a számolási feladatok, és a hőtágulási együttható is bevezetésre kerül. A hőtágulásról is, van egy tapasztalatai tudásunk még mielőtt erről bármit is hallanánk az iskolában, és talán ezért nem foglalkoznak részletesebben a tankönyvek ezzel a fogalommal. De talán mégis kellene, mert Tél Tamás és Horváth Ákos tanár úr szerint a diákok nem tudják a hőtágulást, vagyis a pontos képletre nem igazán emlékeznek, amit viszont már egyetemistáknak tudniuk kellene. Meg kellett volna tanulni még a középiskolában. Lehet, hogy nem csak ezzel vannak így, mert elég sok fogalom a könyvekben, csak említés szintjén szerepel, és nem mélyíti el a tudást a gyerekek fejében.

Egy másik hasonló fogalom az energia, hisz annyit emlegetjük a mindennapi életben és mégse értjük teljesen. Persze lehet, hogy ezzel nem is foglalkoznak annyit a diákok, vagy mondjuk a hétköznapi emberek, mert mindenkiben kialakult egy bizonyos energia kép. Csak azt nem tudjuk, hogy ez a kép nem az amit mi megtanultunk fizikaórán, és gyakran összekeverjük e fogalmakat. Na itt kellene fellépni és tisztázni, hogy a gyerekek könnyebben megértsék, és aztán meg tudják különböztetni, hogy mikor beszélünk hétköznapi és mikor fizikai energiáról.

A munka

A munka jellege, hatásfoka és keretei a történelem során nagyon sokat változott. Kezdetben a munka emberi munka volt. Az ember mindig igyekszik kevesebb fáradsággal életben maradni, ezért megpróbál olyan gépeket előállítani, amelyek a munka testi fárasztó jellegét csökkentik.

A munka fogalma viszonylag későn jelent meg a fizikában. A munka valamilyen célirányos tevékenység. Mindig valamilyen eredményt szeretnénk elérni a munkánkkal, hogy aztán azt, amit létrehoztunk fel, tudjuk használni. A munka jelege a történelem során mindig változott. ( Martinas, 2003)

A munkáról még nem sokat beszéltem a dolgozatom során, pedig tudjuk, hogy a munka is fontos szerepet játszik a termodinamikában. De talán ezt sokkal könnyebben képzelik el a gyerekek és értik meg, mint az energiát. Munkavégzés valamilyen változás megakadályozása. Lehet szellemi vagy fizikai munka, amikor a környezetünkben alakítunk ki változást. Ha munkát végzünk, akkor elfáradunk, ezt tapasztaljuk is. De a munkavégzés és a fáradság között nincs egyértelmű kapcsolat, mert nem mindegy, hogy hogyan végezzük a munkát. Végig kell gondolni, hogy hogyan lenne a legcélszerűbb a változást létrehozni, és hogy ne fáradjunk el túlságosan. Persze ha semmit nem csinálunk, akkor lehet nem fáradunk el, de akkor viszont nem történik meg a kívánt változás.

A gyerekek ezt a munkát tapasztalják, látják és ezzel meg is tanulják a mindennapi életből. A fizikaórákon pedig megtanulják a mechanikai munkát, az elektromos munkát vagy a kémiai munkát. De a fizikakönyvekben mégis a legtöbbet emlegetett munka a mechanikai. Lehet, hogy ennek az, az oka, hogy ez a legkönnyebben kiszámítható?

5. Ábra

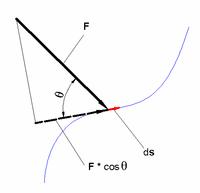
A munka definíciója:

W= F s cos α

A testre hatóerőnek az elmozdulás irányába eső vetületét összeszorozzuk az elmozdulással. Sokszor úgy tűnik, hogy csak ez a munka, hisz a tankönyvek is ezzel foglalkoznak a legtöbbet. A tankönyvek a termodinamikai részében nem nagyon emlegetnek más munkát, de ugye ha ott megnézzük nem kizárólag csak mechanikai munkáról beszélünk, hanem a térfogati munka is szerepel. A tankönyvekben se igazán szerepelnek a munkafogalmak, melyeket vizsgáltam.

A munkát, mint absztrakt fogalmat a közgazdaságban használták először. Termékeny emberi munka volt minden gazdaság forrása Adam Smith szerint és nem kereskedelem, vagy természet, mint ahogy a merkantilisták vagy a fiziokraták állították. Coroilis és Poncelet nyomán a fizikában megjelent a munka 1829-ben. Ők vezették be a kinetikus energiát. (Martinás, 2007)

Termodinamika főtételei

Az első főtétel tudjuk, hogy az energiamegmaradás-át mondja ki. A rendszer által felvet hő egyik része a rendszer energiájának a megváltozására a másik része munkavégzésre fordítódik.

Q=DU+L

Az energiamegmaradás tétele azt mondja ki, hogy az energia megmarad de semmit sem mond a folyamatok irányáról, pedig a termodinamikában a folyamatok bizonyos irányban végbe mennek bizonyos irányban pedig nem. Erre ad felvilágosítást az entrópia fogalma. Ha így mondjuk ki az energia megmaradási törvényt a diákok nagy részének érhetetlenné válik, hisz ez eléggé elvont, és mint már többször is említettem a mindennapi életben nem ezt tapasztaljuk. A mechanikában bevezetett energia megfelel a hétköznapi energia fogalmunknak. A tankönyvekben is ezt az energiamegmaradás törvényt találjuk meg. Az általános iskolás könyvek még ezzel a kérdéssel nem igazán foglalkoznak, vagyis ilyen részletekben nem mennek bele, csak kimondják, hogy megmarad, és nem vész el csak átalakul az egyik formájából a másikba.

Vajon mit mondanak a tankönyvek a második főtételre? Az általános iskolás könyvek csak megemlítik és valahogy tapasztalati tényként, kezelik, persze ez még nincs kihangsúlyozva, hogy ez a termodinamika második főtétele. Míg középiskolában már külön hangsúlyt fektetnek arra, hogy a diákok ezt is megtanulják, „a hő mindig csak a melegebb testről a hidegebb testre megy át.” (Karácsonyi 2003 83. o.) Ha ezt a mondatot elolvassuk, akkor tényleg nem úgy hangzik, mintha valami nagy dolgokat fogalmaznának meg nekünk a második főtételben, hisz ezt tapasztaljuk. De ha úgy fogalmaznánk meg a második főtételt a tankönyveinkben, hogy másodfajú perpetuum mobile működése nem létezik, akkor ez biztos kicsit elgondolkodtatná a gyerekeket. Ilyen megfogalmazásban, egy középiskolás tankönyvben találkoztam, persze itt most csak azokról beszélek melyeket, átnéztem. Itt elmondja, hogy az örök mozgó olyan elven működő gépeket értenek alatta,” mint amilyen a hajó lenne, amely a tengervíz által leadott hőmennyiséget használná a hajócsavar forgatására.”( Pászli 2006 181. o.)

Tehát saját kísérleteik alapján könnyen ki tudják számolni azokat a dolgokat, amelyeket aztán meg is kell tanulniuk. A termodinamikában elég sok új fogalom van, amelyekkel előtte a diákok még nem is találkoztak. Itt most nem arra értem, hogy még nem is halottak róla, hanem, hogy a fizikának az előző részében nem volt még definiálva az a fogalom. Mert a gyerekek már elé sok olyan fogalommal találkoztak, amiről feltételezik, hogy tudják is mit jelent, csak sajnos sokszor teljesen más az elképzelésük egyes fogalommal kapcsolatban, mint ahogy azt a fizikában használni kellene. Ezért kell kitisztítani a gyerekek fejében egyes fogalmak kialakulását, elképzelését és tovább fejlesztését. Egyik ilyen zavaros dolog a sokszor emlegetett energia. Vajon ezt hogy lenne célszerű bevezetni, hogy el tudjuk különíteni a hétköznapi energia fogalomtól. Talán az lenne a legjobb, ha a hétköznapi energia fogalmat valami más néven használnánk. Erről már a fentiekben beszéltem és ez az exergia. Persze most azt gondolnánk, hogy na már megint egy új fogalom, egy új szó amit a diákoknak meg kell tanulniuk, de tényleg így van? Szerintem a definícióját már tudják, hisz használják a mindennapi életben, mert ez az energiaforrásból kinyerhető maximális energia, csak a szót kellene megtanulniuk, és máris különbség lenne két energia fogalom között.

De most inkább arra szeretnék kitérni, hogy a tankönyvekben hogyan is jelenik meg az energia fogalma. Mert mint tudjuk magyarországi felmérések szerint a gyerekek nagyobb része, nem kedveli a fizikát. Ha ranglistát nézzük, akkor a fizika a kémiával karöltve az utolsó helyen van. De vajon miért? Kérdezhetnénk. Nem tudhatjuk pontosan, csak találgathatjuk, de az egyik nagyobb probléma az lehet, hogy a gyerekek nem teljesen értik az energia fogalmát. És ugye, mint tudjuk az energia végig vonul az egész fizikán, és ha ez nem teljesen tiszta a gyerekek fejében, akkor talán az egész fizika egy homályos folt ként lappang a koponyákban. De a fizika mellett ott a kémia is, és ott is sokat használják az energia fogalmat, lehet, hogy tényleg valahol itt kell keresni a probléma megoldását. ( Radnóti )

Először is nézzük a hőtanban oly sokat használt belső energiát, amiről már annyit beszéltünk. A belső energia tanítása elég problémás feladat, nehezen értelmezhető fogalom. Azt már mondtuk, hogy a test ha mozog akkor van mozgási energiája, de ha nyugalomban van, és nincs semmi kölcsönhatás akkor is van energiája. A belső energiának különböző definícióját találjuk meg a tankönyvekben.” Azt az energiát, amelynek változása a hőmérsékletváltozásban mutatkozik meg, belső energiának nevezzük.” ( Karácsonyi 2003 55. o.) Egy másik tankönyv a melegítéshez és hűtéssel magyarázza a belső energiát, mint pl. a Gyulás János és más társszerzők által írt tankönyv. „A testeknek azt az energiáját, amely melegítéssel, illetve hűtéssel megváltoztatható, belső energiának nevezzük.” ( Gulyás 2003 114.o.) Vagy a belső energia változás mértéke attól függ, hogy milyen anyagot használunk, mekkora a tömege, és mennyi a hőmérsékletváltozása. Tehát a ΔE= cmT. Szóval az energia fogalma nem egy egyszerű és kézzelfogható dolog. Elég sok értelemben használjuk az energiát a hétköznapjainkban. Beszélünk a villany energiájáról, mellyel főzünk, vagy fűtünk, de beszélhetünk a mobiltelefon energiájáról, vagy az élet energiáról és még tudnám sorolni a mindennapokban használt energia fogalmakat. Ha megnézzük ezek munkavégzőképességre vagy erőre, utalnak. Ez az energia nem megmaradó mennyiség, hiszen a munkavégzőképesség nem marad meg, hanem elvész. A tapasztalataink is erről győznek meg bennünket. Például a mobil készülék energiája, lemerül, az ember elfárad, energiája elfogy, ezt elég sokszor használjuk, vagy azt hogy már nincs energiánk semmire, de persze bővíthetném még a felsorolásaimat, mert elég tényleg a tapasztalataink során az energia újratermelhető és ugyanakkor el is fogy.

Hétköznapi tapasztalataink szerint a köznyelvi energiát a második főtétellel kötjük össze, ezzel szemben a fizikai energia az első főtételből származik és egy megmaradó mennyiség. A fizikai energia egy absztrakt fogalom, amit elég nehezen értelmezhetünk.

Az energia központi fogalom a fizikában, de úgy szintén a biológiában, a kémiában is megtalálható, és persze még a mindennapi életünk során elég sok helyen hallunk erről a fogalomról. Ezért kell kicsiszolni és különbségeket tenni a különböző energia fogalmak között. Ezért talán megkérdőjelezhető, hogy érdemes-e előszöz mechanikát tanítani a gyerekekkel vagy inkább termodinamikát, hisz a termodinamika törvényei a természettörvényei, és már sok olyan dologgal találkozunk az életünk folyamán, amit a termodinamikában is felfedezhetünk. Talán még az energia fogalmát is könnyebben és érthetőbben be tudjuk vezetni.

Lehet a fizika másik nagy problémája, hogy a matematikai alapok még nem állnak rendelkezésre a tananyag átadásához. A kerettanterv szerint fizikát a 9-11 osztályban tanítják. Ilyenkor a gyerekek nem tanultak még másodfokú függvényekről, vagy mondjuk szögfüggvényekről, és ezekre szükség lenne a mechanikában. De most megpróbálják úgy kialakítani a feladatokat, hogy ezekre ne legyen szükségük a diákoknak. A termodinamikát, mint már említettem a hőmérséklettel kezdik el, majd a hőtágulásokkal folytatják és ilyenkor már szerencsés, ha a gyerek rendelkezik mechanikai tapasztalatokkal. A termodinamikában már a nyomás fogalma is előkerül és itt, viszont szükség van az erőre is, mint fizikai mennyiségre, amit viszont jó ha már a mechanikai részben megtanulnak a gyerekek.

A másik probléma a termodinamika statisztikus értelmezésével van. A nyomás a hőmérséklet értelmezhetetlen statisztikus módon, ha előbb nem ismerjük meg a mechanikában. De ezek statisztikus magyarázata elkerülhetetlen a fizikai világkép kialakulásához. Szóval megvizsgálhatjuk, hogy mi lenne jobb, és hogy melyik anyagrész legyen az, amit először megtanítunk a gyerekeknek, de valahogy mindig hiányosságokba ütközünk. Például, ha statisztikus módon szeretnénk bevezetni a termodinamikát, akkor nehézségekbe ütközünk, mert a 9.-es gyerekek valószínűség számítási ismeretei nem eléggé fejlettek ennek az elsajátításához, mert a természeti törvényeket, mint valószínűségi törvényeket mutatja be. De a fenomenológikus termodinamika nem statisztikus törvényekkel operál, ezért a természettudományos világkép kialakításához ez problémás lehet.

A hő és a hőmérséklet a tankönyvekben

A termodinamikát a tankönyvek először a hőmérséklet bevezetésével kezdik. Vagyis inkább egy ismertetést közölnek olyan kísérleteken keresztül, amit már a tapasztalataikból megtanultak a gyerekek. Mintha feltételeznék, hogy a hőmérséklet és ezzel együtt a hő is nagyon jól ismert fogalom a gyerekek részére és ezt nem kell külön definiálni. Sokszor viszont a hő és a hőmérséklet fogalmát se különböztetik meg. Ez viszont elég sok bonyodalmat okozhat a gyerekek további tanulmányaiban. Egyik tankönyvekben az áll, hogy a hőmérsékletet kezünkkel érezzük és ezzel még pontos adatokat, nem tudunk mondani, csak akkor, ha a hőmérőről leolvassuk a számadatot.( Zátonyi, 2006, 135. o.) Szóval a hőmérsékletet kísérletekkel, tapasztalati útón vezetik be a tankönyvek.

Tehát mint látjuk a hőre, találunk definíciókat, míg a hőmérsékletre ilyen konkrét definíciót nem adnak a tankönyvek. De talán, ha a fentebb említett kísérletet meg csinálják, akkor talán világosabbá válik számukra, a hőmérséklet és a hő fogalma, valamint a kettő közötti különbség. Itt nem kritizálni akarom a tankönyveket, mert mindegyik jó és érdekes a maga módján, és biztos nem is olyan egyszerű egy ilyen tankönyvet megírni, sőt biztos vagyok benne, hogy nagyon sok munkával jár. Csak lehet, hogy mivel olyan sok az anyag ezért valahogy be kell osztani, hogy mire fektetnek nagyobb hangsúlyt és mire nem. De lehet, hogy pont azokon az alapfogalmakon surranunk át, amelyeket érdemes lenne tisztázni, mert erre alapozzák a későbbi tudást. Lehet, hogy tényleg triviálisnak tűnik, és mindenki tudja, hogy mi a hőmérséklet.

Egyes ismereteinket tapasztalatunk útján szerezzük, és úgy gondoljuk, ezekkel nem kell annyit foglalkozni, az órán. Mindenki tudja, hogyha valamit melegítünk, akkor annak megváltozik a térfogata. Már biztos minden gyerek kipróbált valami szilárd testet melegíteni és tudja, hogy akkor annak térfogata megnő, ha hűtjük, akkor pedig összehúzódik. Tehát ezt is tudjuk tapasztalatból, de azért fizika órán erre is külön kitérünk, és kísérleteket végzünk, hogy a gyerekek minél jobban megértsék. Ha körbenézünk a környezetünkben, mindenhol ott van körülöttünk a fizika, és minden olyan triviálisnak és egyszerűnek tűnik. Akkor miért van, hogy fizikaórán mindenki újnak és ismeretlennek titulálja az anyagot? Talán, azért mert akkor azt gondoljuk, hogy az amit ott órán tanulunk az csak is bonyolult lehet. Pedig ha leegyszerűsítjük a dolgokat és a hétköznapi tapasztalatok alapján, magyarázzuk meg őket akkor érthetőbbé, válnak, és közelebb kerülnek a diákokhoz.

Tehát a gyerekek sokszor már attól a szótól megijednek, hogy fizika. Gyakran olyan egyszerű kérdésekre nem tudnak válaszolni, amire nem fizikaórán könnyen tudnák a választ. Ilyen egyik példa, a sárosdi Farkas Gyula emlékére rendezett fizikaversenyen a gyerekeknek meg kellett magyarázni a jelenséget: ha a hőmérőt beletesszük forró vízbe, akkor a higany előbb lesüllyed, és utána emelkedik. Voltak, akik megadták a helyes választ, de azért nagyobb részük nem tudta pontosan megmagyarázni, hogy mi is történik akkor. Voltak olyanok is, akik gondolkoztak és hétköznapi tapasztalataik alapján, próbálták megmagyarázni a jelenséget. Persze nem teljesen helyesen, de próbálkoztak. Az ő megoldásuk, úgy szólt, hogy ha mi is belenyúlunk a forró vízbe, akkor először hidegnek érezzük azt és csak utána melegnek. Valamilyen szinten igazat mondtak és látszott, hogy gondolkoznak, de itt nem ez volt a válasz és itt ők a hőáramról beszéltek. Voltak olyanok is akik az endoterm és exoterm hatással magyarázták a jelenséget: „ Ha a hőmérőt forró vízbe mártjuk, illetve sokáig bent tartjuk, akkor a higanytól hőt nyel el, amit endoterm hatásnak nevezünk. Kicsit lemegy a higanyszál és utána hirtelen meg fog emelkedni. Ennek oka, hogy a forró víz hőt ad át a higanynak, amit exoterm hatásnak nevezünk.” Csak egy részét idéztem annak, amit a gyerekek leírtak a versenyen. A megfogalmazás, jó csak sajnos a válasz nem. A helyes válasz az lett volna, hogy először az üveg tágul ki és ezért esik le a higany szintje, és utána mikor átveszi a hőmérsékletet akkor kezd emelkedni. Itt is látszott, hogy egyesek gondolkodnak és megpróbálnak a tapasztalataikra hagyatkozni, míg mások olyan fizikai kifejezéseket kerestek, melyek jól hangzanak. Sokszor nagyon egyszerű dolgokat is túlbonyolítunk fizikaórán, másokat viszont feltételezik, hogy már tudják a diákok, és nem nagyon foglalkoznak velük.

Egy másik hasonló fogalom az energia, hisz annyit emlegetjük a mindennapi életben, és mégse értjük teljesen. Persze lehet, hogy ezzel nem is foglalkoznak annyit a diákok, vagy mondjuk a hétköznapi emberek, mert mindenkiben kialakult egy bizonyos energia kép. Csak azt nem tudjuk, hogy ez a kép nem az amit mi megtanultunk fizikaórán, és gyakran összekeverjük e fogalmakat. Na itt kellene fellépni és tisztázni, hogy a gyerekek könnyebben megértsék, és aztán meg tudják különböztetni, hogy mikor beszélünk hétköznapi és mikor fizikai energiáról.

Az exergia

Ahhoz, hogy meg tudjuk különböztetni a hétköznapi és fizikai energia fogalmunkat, egy új fogalmat kell bevezetni, mely a hétköznapi energia szóhasználat helyett alkalmazható, ez pedig az exergia.

Exergiának egy rendszerből kinyerhető maximális munkát nevezzük. Mikor végezhetünk munkát? Ha a rendszer nincs egyensúlyban a környezetével. Ezt mondja ki a második főtétel is, és a hétköznapi tapasztalatunk is ezt mutatják. Egy rendszer akkor végezhet több munkát, ha minél távolabb van a környezete egyensúlyától.

De nézzünk egy példát az exergiára, amit talán a középiskolások is megérthetnek. Vízesésnél a lezúduló víz nincs egyensúlyban a környezetével, ezért mondhatjuk, hogy munkát végez, tehát egy bizonyos mennyiségű exergiával rendelkezik. De a leérkezett víz ugye már nem rendelkezik exergiával, nem nyerhetünk belőle energiát, munkavégzésre nem hasznosítható. A vízesés tetején lévő víz viszont annál inkább, ideális esetben a vízesésből

E= mg ( h₁ – h₂)

helyzeti energia fordítható munkavégzésre, tehát ez az exergiája.

Ugyanakkor megvizsgálhatjuk egy T₁ hőmérsékletű test exergiáját, T₂ környezethez képest. A test belső energiája felírható:

E₁= cT₁

A T₂ hőmérsékleten az energia:

E₂ = cT₂

Az exergia viszont a rendszer és környezet energiájának többlete az egyensúlyi állapothoz képest, azaz

B = c ( T₁– T₂)²/T2

Ugyanakkor figyelnünk kell arra, hogy az exergia nem az energia része. Az exergia munkavégző képesség míg az energia megmaradó mennyiség. Az energia mechanikán keresztül történő bevezetése gyakran vezet arra a következtetésre, hogy a munkavégzőképesség ( a felhasználható energia) a az energia része, erre azért figyelnünk kell és igyekezni elkerülni. (Martinás 2003)

A termodinamikai fogalmak kialakulásának története

Termodinamika teljesen a hétköznapi tapasztalatainkról szól, sok olyan fogalommal találkozunk, melyeket a hétköznapjainkban is használunk. Amit látjuk nagyon hosszú fejlődés eredménye e fogalmak kialakulása. Ilyenek pl. a hőmérséklet, hő, energia ( entrópia).

A tanításban az a feladatunk, hogy megteremtsük a hétköznapi és a tudományos fogalmak közötti kapcsolatot. Hogy felhívjuk a figyelmet arra például, hogy a hőmérséklet nem az a szám, amit a hőmérő mutat, hanem egy állapotjelző.

A termodinamika felépítését valahogy a történethez kellene alakítani, és felhívni a diákok figyelmét egyes fogalmak kialakulására, akkor talán nekik is világosabbak lennének az új fogalmak és a törvények.

A testek bármilyen, a hőmérséklettől függő tulajdonsága felhasználható hőmérő készítésére. Galilei alkotta meg az első hőmérőt, melynek még nem volt skálája. Leggyakrabban a folyadékok hőtágulását használták fel. A hőmérő megjelenésével, és annak alkalmazásával, viszont ki tudták küszöbölni a hőjelenségek becslését, és pontosabb mérési eljárást kaptak.

De viszont a test hőmérsékletének meghatározására a lázmérőt, már 1612-ben alkalmazták. Egy padovai orvos, Sanctorius alkalmazta a hőmérőt, úgy gondolta, hogy az emberek testhőmérsékletének ingadozása, az különböző betegségeket jelent. Az akkori lázmérő egy üveggömbből állt mely levegővel, volt megtöltve és egy csőből, mely pedig folyadékkal volt megtöltve. Itt a gömböt vették a szájukba a betegek, és ha hőmérséklet emelkedése volt, akkor a csőben a folyadék szint nőni kezdett.

Az egyik első fix pont az emberi szájban mért hőmérséklet volt, Newton ezt használta a lehűlési törvényének mérésekor. Különböző kivitelű és skálabeosztású hőmérőket konstruáltak, egyik közismert a higanyhőmérő Celsius-féle hőmérsékleti skálája.(1742). De mások is készítettek különböző skálákat ilyenek a Fahrenheit- féle skála, melynek a beosztása 32^oF – tól 212^oF- ig terjed, valamint a Réamur – féle skála melyen 0^oR^–80^o R–ig terjedő beosztás található. ( Budó 1997)

Ezek után már tényleg pontos értékeket tudtak mondani a hőmérsékletre és nem csak becsléseket. A hétköznapi életben sokszor mondjuk valamire, hogy fagyos, vagy hűvös vagy meleg stb. de ezek mint csak empirikus skálák ha azt nézzük és attól függ mihez viszonyítjuk ezeket a megállapításainkat. Tehát ezek valaminek a becslésszerű értékére utalnak, hol hőmérsékletre, hol hőmennyiségre, hol esetleg valami másra. Tehát a hőmennyiség fogalma elég problematikus, mert sokszor keveredik a belső energia fogalmával. A 17. században azt állították, hogy a hő a testek részecskéinek mozgásából ered.

Az 1760-as években Joseph Black megalkotta a hőmennyiséget és a hőmérsékletet a hőállapotnak a felbontásából. A köznapi szemlélet a hőt önálló létezőnek tekinti.. Black vezette be a fajhő és a latens hő fogalmát.

William Cleghorn 1779-ben a következő posztulátumokat alkalmazta a termikus jelenségek meghatározására:

„1. A kalorikum egy rugalmas folyadék, amelynek részecskéi taszítják egymást,

2. A kalorikum részecskéket a különböző anyagok a különböző állapotokban, különböző mértékben vonzzák,

3. A kalorikum nem keletkezik, és nem tűnhet el,

4. A kalorikum érzékelhető vagy látens alakban jelenik meg. A látens kalorikum olyan kalorikum, amely kémiailag kombinálódik a szilárd anyag részecskéivel s így az folyadékká válik, vagy a folyadék részecskékkel s azok gázzá válnak,

5. A kalorikumnak súlya van.” ( Martinás)

Watt 1769-ben mutatta be a gőzgépet, de nem ő találta fel, ő csak tökéletesítette. A gőzgép az ipari forradalom legfontosabb gépe lett, ugyanakkor ennek tanulmányozása előre vetítette az anyag és a mozgás tanulmányozását. ( Szabó 2003)

7.Ábra

Lavoisier és Laplace a hőelmélet alapjait kezdték el szisztematikusan vizsgálni, a munkájuk elején két hőelméletet állapítottak meg, az egyik a vis viva, vagy kinetikus elmélet, mely a surlódásos hő keletkezését jól értelmezi. A másik a kalorikum elmélet mely szerint a hő anyagi folyadék. A kettő között nem döntöttek, de azt megállapították, hogy a hő megmarad.

A 18. században Lavoisier a hőanyagelmélet alapján kidolgozta a kalorimetriát. és megdöntötte az égéssel kapcsolatos flogisztonelméletet. Ez volt az az elmélet mely minden oxidációs jelenséget egységesként próbált értelmezni. Minden olyan test mely égésre képes tartalmaz egy éghető anyagot a flogisztont, mely ezt az éghetőséget biztosítja, és minél többet tartalmaz egy anyag annál könnyebben és hevesebben ég.

Sadi Carnot (1796 – 1832) volt az egyike azon kutatóknak, akik a gőzgép tanulmányozásával foglalkoztak. Tanulmányozásai sorát kimutatta, hogy a gőzgép üzemeltetését biztosító hőnek csak egy bizonyos része alakul át hasznos munkává. Bevezette a reverzibilis folyamatok fogalmát. Carnot elég fiatalon elhunyt munkái, halála után jelentek meg és akkor fedezték fel egyik feljegyzését is melyben az energiamegmaradás törvényét fogalmazta meg.

Kitérnék egy kicsit részletesebben Sadi Carnot hő fogalmára.

Carnot a kalorikum híve volt, számára a hő megmaradó mennyiség. Korszakalkotó művét úgy írta meg, hogy bátyja Hippolite is megértse, aki nem rendelkezett műszaki ismeretekkel. A dolgozatában a melegségről, a gőzgépről beszél, ugyanakkor azt is vizsgálja, hogy az adott hő által végzett munka függhet-e a közvetítő anyagtól. Munkájában mozgatóerőről beszél, egységének azt értette, ami 1 kg tömegű testet 1 méter magasra tud emelni. Ma már a mozgatóerőt munkának nevezzük.

Vizsgáljunk egy p₁= 0.2 MPa nyomású és V₁= 1 m³ térfogatú gázt, amely p₀= 0,1 MPa nyomású szobában van. A gáz kitágul, és a tágulás során munkát végez, és hőt vesz fel. Egész addig, amíg a nyomása p₂=0.1 MPa és térfogata V₂=2 m³ lesz, eközben L= 0.6 MJ munkát végez.

L = p₁ V₁ ln = 2 ln2 MJ=60 kJ

A folyamat közben hőt vesz fel és ez mérhető. A mérések után azt tapasztaljuk, hogy a felvett hő arányos a munkával. Ahhoz, hogy újból munkát tudjunk végezni a gázzal vissza, kell állítani eredeti, azaz kezdeti állapotába. Vagyis össze kell nyomni, amihez viszont munkát kell végezni, ez pedig függ a hőmérséklettől. Az általános gáztörvényt használva erről meggyőződhetünk pV = nRT ahol R a gázállandó. Ezek után számolva:

L =n R T₁ ln = 2 ln2 MJ=60 kJ

Ha a térfogatot a felére csökkentjük, akkor ehhez T₂ hőmérsékleten

L₂ = n R T₂ ln2 = 60 kJ

Ha az összenyomást alacsonyam hőmérsékleten végezzük, akkor kevesebb munkát kell befektetni. Tágítás során pedig munkát nyerünk, és ennek egy részét fel tudjuk használni az összenyomásra, hogy visszajussunk a kiinduló állapotba. A hasznos munka annál több minél nagyobb a hőmérséklet különbség a tágítás és az összenyomás között. Ha nincs különbség, akkor nincs hasznos munka.

Megvizsgálta, hogy mi történik akkor, ha nem gázzal, hanem valami mással mondjuk vízgőzzel, végezné el a kísérletet, vagy mondjuk más típusú munkát, használna. Könnyen megvalósítható, hogy nem nyer ki hasznos munkát. Tehát ez a minimum, de vajon van-e maxmimum és ez mitől függ, tehát tulajdonképpen azt a kérdést tette fel, hogy ad-e a természet korlátot.

Nézzük a hűtőgépet, itt az összenyomást magasabb hőmérsékleten végezzük, akkor több munkát kell befektetni, de a gáz alacsonyabb hőmérsékleten veszi fel a hőt, és magasabbon adja le. Ha ezt a hűtőgépet összekapcsoljuk egy géppel, akkor a gép felvesz Q₁ hőt, és L₁ munkát végez, ezt pedig a hűtőgépbe tápláljuk, amely Q₂ hőt ad le magasabb hőmérsékleten.

Tapasztalataink azt mondják, hogy a leadott hő nem lehet nagyobb, a felvetnél. Ellenkező esetben egy változás történik, az alacsonyabb hőmérsékletű rendszer lehűl, a magasabb pedig még magasabb lesz. A hőmérsékletnek az a tulajdonsága, hogy a létező hőmérséklet különbségek eltűnnek, azaz kiegyenlítődik a két rendszer hőmérséklete. Ekkor viszont nem lenne hőmérő. Ugyanakkor, ha ez fenn állna, akkor egy olyan gépet tudnánk előállítani, amelyik a semmiből állítana elő munkát, és a fennmaradó hővel egy újabb gépet tudna örökké működtetni.

A leadott hő lehet kisebb, mint a felvett, a maximálisan leadott pedig megközelítheti a felvetett. Ez egy olyan hűtőgép, amely visszafelé megismétli a gép működését és ezt reverzibilis gépnek, hívjuk. Ez a reverzibilis gép adja a maximális hasznos munkát, de ilyen a valóságban nincs. A maximális hasznos munka kinyerése csak a hőmérséklettől függ, ez viszont minden reverzibilis gépre azonos, ha nem így lenne, akkor perpetuum mobilet kapnánk.

Sadi Carnot kiszámolta a maximális hasznos munkát:

"Levegő esetén 1000 egység melegség, ha a meleg 1 meleg testről 0 hőmérsékletűbe megy át 1.395 mozgató erő‑egységet hoz létre, gőz esetén 1000 egység melegség, ha a meleg 100 meleg testről 99 hőmérsékletűbe megy át 1.112 mozgató erő‑egységet hoz létre. Gőz (1 és 0 között) 1.212 mozgató erő‑egységet hoz létre, A borszesz (100 és 99 között) 1,212 mozgató erő‑egységet hoz létre." ( Sadi Carnot)

"Még több ilyen számítást is szerettünk volna végezni, a jelenlegi fizika megtagadja tőlünk az erre nézve szükséges adatokat". (Sadi Carnot)

1834‑ben, Emile Clapeyron (1799‑1864) egyik dolgozatában reprodukálta Carnot gondolatat menetét, azzal a különbséggel, hogy az összefüggéseket matematizálta és a Watt – féle indikátor diagrammal ábrázolta a körfolyamatot. Ennek segítségével dolgozza ki Kelvin és Clausisus a modern termodinamika alapjait.

Kelvin a 1852-ben a Kelvin skálát Carnot eredményei alapján vezette be. Úgy vélte, hogy Carnot elmélete, amely a hő mozgatóereje vonatkozik, lehetővé teszi, egy olyan elv megalapozását, amelyre az abszolút hőmérsékleti skála alapozható.

Hogy a hő mechanikai hatást váltson ki – a valódi gépekben- ahhoz egy erőforrást kell keresnünk a hőátadás során. Mechanikai hatáshoz úgy juthatunk, ha meleg testből leengedjük a hőt a hidegbe, visszafelé is megmutatta ugyan ezt. „Az adott mennyiségű hő átadásával kapott mechanikai hatás, ha a hőátadás tetszőleges típusú, tökéletes hatásfokú gép közegében zajlik, amint Carnot megmutatja, a gép hőátadásra használt anyagának jellegétől független, és csak annak a két testnek a hőmérséklet-különbségétől függ, amely között a hőátadás zajlik.” ( Martinás)

A valódi gép hatásfoka, mindig kisebb, mint:

Ha a hőmérséklet skáláját úgy határozzuk meg, hogy a hatásfoka a fenti kifejezésre legyen érvényes, akkor a termodinamika törvényei a legegyszerűbb alkot, veszik fel.

Az energiamegmaradás törvénye három személy nevéhez fűződik: Julius Robert Mayer (1814 – 1878), James Joule (1818 – 1889) és Herman von Helmoltz (1821 – 1894). Mayer és Helmoltz az „erők megmaradását” javasolta, nem igazán ismerték a kalorikum elméletet, ők a vis vitalis ellen harcoltak. Az orvosokat az érdekelte, hogy teljesülnek-e az élő szervezetben a fizika és a kémia törvényszerűségei. Helmoltz megközelítése az volt, hogy a vis vitalis valóságos perpetuum mobile volna. Ugyanis a perpetuum mobiletől azt várjuk, hogy munkát produkáljon a semmiből, vagy kevesebb munkával többet végezzünk.”A vis vitalis elmélet szerint az életerő feladata a szervezet rendeltetésének megfelelően a fizikai és kémiai erők szabályozása volt.” (Martinás) Ez a fizikai törvények korlátozását, vagy megszüntetését is jelentette.

Helmholtz „Az erő megmaradása” című értekezését, 1847-ben mutatta be, a berlini fizika társaságában. De a fizikusok kétségbe vonták állításának helyes voltát, csak Jacobi állt ki mellette voltak, akik túl filozofikusnak találták, ezért az előadás csak saját kiadásban jelenhetett meg.

Helmholtznak a zárt rendszerekre kimondott energia tétele a természettudományok alaptételévé vált. Tehát a fizika és a kémia tételei érvényesek az élő szervezetekben is és nincs olyan vis vitalis, ami ezt fölül irná, így született meg az energia tétele.

Joule kimérte a hő és a munka arányát. Ha rögzítjük a kezdeti és a végállapotokat, akkor a Q hőközlés és az L munkavégzés összege állandó marad. Ez úgy értelmezhető, hogy a két test kölcsönhatása leírható energia átadással. Az energia átadásnak két tiszta formája van, az egyik mikor nincs munkavégzés, a másik pedig mikor csak munkavégzés van. A valóságban mindig a kettő közötti eset fordul elő. Úgy is megfogalmazhatjuk, hogy: van egy, a test állapotára jellemző U mennyiség, amelynek megváltozása a rendszerrel közölt Q hő és a rendszeren végzett L munka összege,

DU = DQ + DL

Rudolf Clausius (1822 - 1888) 1867- be bevezeti az entrópia fogalmát., Sadi Carnot (1796 – 1832) munkájának felhasználásával.

A második főtétel megfogalmazása: „a hő soha sem megy magától hidegebb helyről melegebb helyre.” A második főtétel segítségével fogalmazzuk meg az entrópia függvényt:

Rankinek köszönhető a termodinamika és az energia egymásra találása, aki 1855-ben „Az energetika tudomány körvonalai” címmel írta egyik dolgozatát, melyben a modern termodinamikai formalizmus elemei megtalálhatók. De több elnevezési javaslatát a tudomány nem fogadta el.

A gond a hő munkává alakításában rejlett. A hő-munka átalakítás nem szimmetrikus. A két munkafogalom között van egy kis különbség, az egyik az mikor a testen végzett munkáról beszélünk a másik mikor a test végzi a munkát. Az előbbi az energia változás az utóbbi pedig a test energiaváltozása a fizikusok szerint, és hasznos munka a mérnökök szerint.

Az energia az aktuális energia és a potenciális energia összegéből áll. A Rankine-i energia fogalom két irányban fejlődött. Ebből lett a fizikai energiafogalom. Az aktuális energia a kinetikus lett (), az mgh pedig a potenciális energia. Kelvin bevezette a belső energiát, és ezzel a teljes energia:

A belső energia megmaradása azt jelenti, hogy nem készíthetünk olyan gépet, amely semmiből munkát állít elő. Ez az I. fajú perpetuum mobile lehetetlenségének elve

Az energia fogalom története:

Az energia szó eredte a görögök korába nyúlik vissza. Az energia görögül ενεργεια ahol az εν jelentése „be” az έργον-é pedig „munka”,az -ια pedig absztarkt főnevet képez. Az ενεργεια az ógörög nyelvben „ isteni tettet” vagy „bűvös cselekedetet jelentet” Arisztotelész később „ténykedés, művelet„ értelmében használta, energeia néven.( www.wikipédia.org) „Amely a működésben levő képesség, a változás képessége és a változásra való képesség.”( Martinas) Ez inkább a hétköznapi energiára jellemző, míg a fizikai inkább elvont .

1807-ben Thomas Youngnál (1773-1829) jelent meg az energia, mint fizikai mennyiség. Ő a vis viva fogalmát próbálta meg felváltani vele és nem a mai értelemben használta. Kinetikus energiát értett alatta, de még nem alkalmazta a ma már olyan jól ismert képletet. 1829-ben a munka és az energia fogalmat a mai tudományos jelentésében Gaspar Gustav de Coriolis (1792 – 1843) és Jean Victor Poncelet (1788-1867) vezette be először, egyik dolgozatban. Valamint felírták a mozgási energia változás és a munka kapcsolatát, de ez még nem a mechanikai energiamegmaradás volt, csak a mozgási energia és a munka kapcsolata. Rankie vezette be a termodinamikába az energiát, mint munkavégző képességet, és a modern energia fogalom is az ő nevéhez fűződik.

Az energia, mint a rendszer munkavégző képessége, így értelmezhető:

Mennyi munkával lehet a rendszert előállítani egy referencia állapotból – ez a fizikai energia

Mennyi a rendszer változtatási képessége egy adott helyzetben (környezetben)– ez az exergia

Mennyi a rendszer célirányos az ember számára felhasználható változtatási képessége – gazdasági munkavégző - képesség

James Prescott Joule kísérletezései során megállapította, hogy ha egy testet szeretnénk felmelegíteni egy T₁ hőmérsékletről T₂ magasabb hőmérsékletre, akkor ezt hőközléssel vagy munkavégzéssel tudjuk megtenni.

Joul kísérleteiből következik, hogy van a testre jellemző mennyiség, melynek megváltozása:

dU = Q+L

Az energeia nem jelent meg a 19. századi termodinamikában, mint munkavégzőképesség, majd ezt követően a tankönyvekben sem. Valójában a 20. század második felében dolgozták ki a termodinamikában az Arisztotelész által emlegetett energeia megfelelőjét, mert a mérnököknek szükségvolt a tényleges munkavégzőképesség kifejezésére, és ezt nevezték el exergiának. Az exergia a rendszerből kinyerhető maximális munkát méri. ( Martinás -2007 )Az exergia változása:

Energia és exergia tanítása

A következőkben egy-egyszerűbb és érthetőbb bevezetést mutatok be, amellyel könnyebb lenne bevezetni az energia fogalmát az általános iskolában. Egy olyan levezetést mutatok az energiáról, amivel azt a gyerekek is megértik. Ugyanakkor különbséget szeretnék tenni az ő elképzelésükben létező energia és a fizikaórán elhangzó energia fogalmak között. Ehhez szükség van egy új fogalom bevezetésére, hogy meg tudjuk különböztetni a két energia fogalmat. Ez az új fogalom pedig az exergia. Az exergia „a rendszerből kinyerhető maximális mechanikai munkát méri, adott T₀hőmérsékletű környezetben.” ( Martinás, 2007 ) Tehát ez a ténylegesen felhasználható energia, ami a gyerekek elképzeléseiben is megvan, valamint a hétköznapi életben is használjuk. Ezért lenne egyszerűbb az energia- képünk, ha ezt is bevezetjük.

Tudjuk, hogy létezik egy didaktikai szabály, miszerint a diákok minél kevesebb új fogalmat tanulhatnak, ezért a tanárok és a tankönyv írok, megpróbálják a fogalmakat minimalizálni amennyire, csak lehet. De ha visszatekintünk a dolgozatomban, láthatjuk, hogy a fogalmak száma elég sok. Vagy csak nekem tűnik annak? Arra szeretném felhívni a figyelmet, hogy ha már úgy is annyi mindent megtanítunk a gyerekeknek, akkor miért ne lehetne még egy új fogalmat bevezetni, amely elősegítené az energia megértését. Kétségtelen, hogy egy új fogalom bevezetése nem egy egyszerű dolog, ha ez tényleg elősegítené egy olyan fogalom kitisztulását, és a fogalomzavarok elkerülését, ami fontos a fizikában, akkor talán megérné tenni érte. Az exergia bevezetése fontos lenne, hogy rendbe rakjuk a fizika, biológia, földrajz órán tanult energia fogalmakat.

Több energia fogalom létezik, van a hétköznapi, amit a biológia vagy földrajz órán tanulnak a gyerekek és a fizikai, amit fizika órán. Az utóbbi a megmaradó mennyiség és az első főtételhez kapcsolódik, a hétköznapi pedig inkább a második főtételhez kapcsolható. Mint már említettem a hétköznapi energiához, mint fizikai mennyiséget az exergiát rendelhetjük hozzá. Mindig megadja, hogy a rendszerből mennyi munka nyerhető. A fizikai energia pedig egyik rendszerből áramlik egy másikba és ez jellemzi a fizikai folyamatot, amely viszont egy megmaradó mennyiség. Elég nehéz az energiát úgy megtanítani, hogy az energia és az exergia két elkülöníthető fogalom legyen. De azért megpróbálok két különböző utat vázolni, amivel mindkettő bevezethető.

Az exergia bevezetése

A bevezetést egyszerű példákkal lehetne kezdeni a fizika órán. Ez nem is lenne olyan bonyolult, mert a hétköznapi energia fogalmunknak megfelelő fizikai mennyiség az exergia. Ezért a példák felsorolása nem okozna problémát. Tulajdonképpen ezt a fogalmat használjuk a mindennapjainkban is csak, mint energia. Ezért arra kellene felhívni a diákok figyelmét, hogy ez nem egyezik meg a fizikai energiával.

A legjobb lenne, ha a diákok mondanának példákat saját tapasztalataik alapján, de tulajdonképpen mi is segíthetünk nekik. Megkérdezhetjük, hogy ha a szobában a radiátor, vagy a kályha ugyanolyan hőmérsékletű lenne, mint a szoba akkor fel tudnánk-e melegíteni a szobát? Erre minden gyerek tudná a helyes választ, azaz nem tudná felmelegíteni a szobát. Egy másik példa: Hol építenek erőműveket, egy tónál vagy egy gyors folyású folyóparton? Ugye erre is tudják a helyes választ, hogy a folyón építenek erőműveket, hiszen a tó energiája nem hasznosítható. Itt sorolhatunk még példákat a gyerekekkel együtt, majd a végén meg kell magyaráznunk a jelenségeket, és bevezetni az új fogalmat.

Mint tudjuk, ha a radiátor és a kályha ugyanolyan hőmérsékleten van, mint a szoba akkor az, nem melegítheti fel a szobát, mert az egyensúlyban vannak. A tóhoz nem építhetek erőművet, mert a tó energiája nem hasznosítható. Megnézhetjük, hogy mi a közös ezekben, a példákban. Mint látjuk, ha valami egyensúlyban van, akkor nincs munkavégzés, munkát pedig csak akkor végezhet valami, ha nincs egyensúlyban a környezetével és annál több munkát, végezhet, minél távolabb van a környezete egyensúlyától.

Csak ez után mondjuk el, hogy a példánk során azt néztük, hogy miből lehet a legtöbb mechanikai munkát kinyerni, és ezt nevezzük exergiának. Tehát akkor az elmondottak alapján az exergia arányos az egyensúlytól való távolsággal.

Ha egy lesújtó kalapáccsal minél magasabbról ütjük a szöget az annál mélyebben, megy deszkába, így több munkát végez. A bizonyos magasságból lezúduló víz, mozgásba hozza a vízimalom kerekét. Ezek után sorolhatunk még példákat a napjainkból, de hogy könnyebben megértsék az exergia fogalmát, nézzünk egy konkrétabb példát.

Tehát az előzőekben már közösen megállapítottuk, hogy az exergia függ a magasságtól, tehát minél magasabbról ejtünk egy testet, vagy minél magasabbról zúdul le a víz annál több munkát, végez. Az exergiát B-vel jelöljük, akkor felírhatjuk, hogy B ~ h , ahol h – val jelöljük a magasságot. De egy lezúduló test munkavégző képessége nyilvánvalóan függ a test tömegétől is. Ezt a gyerekek is tudják, hisz nem mindegy, hogy milyen vagy mekkora kalapáccsal ütök be egy szöget, vagy mondjuk a lezúduló víz mennyisége sem mindegy. Mikor már ezt is megállapítottuk ezek után felírhatjuk B ~ hm , ahol m a test tömege.

A gyerekek már remélhetőleg megtanulták , hogy Magyarországon a Föld közelében a gravitációs gyorsulás g=9,81 m/s² A gravitációs gyorsulás tulajdonképpen az a mennyiség, amely az adott bolygó felszínéhez vonzza a testeket. Ezek után az elvi munkavégző képesség a következőképpen adódik:

B=mgh

Ez az új mennyiség az exergia mértékegysége pedig [J]. Fontos megemlíteni, hogy egy rendszerből ennyi munkát valójában soha nem tudunk kinyerni. A folyamat során ennek jelentős része elvész. Ezért az exergia mindig az elvileg kinyerhető munkát jelenti. El kell mondani, hogy azonos tömeg esetén az energia csak a magasságtól függ. Ugyanakkor már arról is volt szó, hogy az exergia az egyensúlytól, való távolságtól függ, és minél messzebb van ettől az egyensúlytól annál nagyobb, ami annyit jelent, hogy annál több munkát nyerhetünk ki belőle.

Ugyan így végig nézhetünk egy másik példát is, ami a mozgásra vonatkozik. A gyerekek már azt is tudják, hogy egy álló vasúti kocsit, egy másik álló vasúti kocsi nem hozhat mozgásba. Egy nyugalomban lévő kocsit csak egy mozgásban lévő másik kocsi indíthat el. Tehát a mozgó kocsinak a mozgási energiája: , ami egyben az exergiával egyezik meg, mivel koordináta rendszerünk a környezethez kötött. Ezt is le lehetne vezetni és még kísérlettel is bemutatni, hogy mitől is függ egy mozgásban lévő kocsinak az exergiája. Egy egyszerű kísérlettel, ha mondjuk egy lejtősen elhelyezett sín végéhez egy másikat helyezünk vízszintesen. A vízszintes sín kezdetéhez egy kiskocsit helyezünk. Ezután a ferde sín egy meghatározott pontjából különböző tömegű kiskocsikat engedünk le. Mivel mindegyik kiskocsit ugyanabból a pontból engedtük le, és mivel a gravitációs mező a tömegtől függetlenül egyforma gyorsulással mozgatja őket, ezért mindegyik ugyanazzal a sebességgel ütközik a vízszintes sín végén levő kiskocsinak. Megfigyelhetjük, hogy a legnagyobb tömegű kiskocsi löki legmesszebbre a másik nyugalomban lévő kocsit.

Ezután ugyanazt a kiskocsit, a ferde sín különböző pontjából engedjük le. Megfigyelhetjük, hogy a kocsi akkor löki legmesszebbre a nyugalomban lévő kocsit, ha a ferde sín legmagasabb pontjából engedtük le, vagyis amikor a legnagyobb sebességgel érkezik le.

A kísérletből tehát megállapítottuk, hogy azonos sebesség mellett a nagyobb tömegű testnek nagyobb az exergiája, azonos tömeg mellett pedig a nagyobb sebességű testnek nagyobb.

Az energia bevezetése:

Az energiával kapcsolatos információink arra mutatnak rá, hogy egy folyamatban mi történhet meg és mi nem. Talán ez az egyik legfontosabb fizikai fogalom melyre oda kell figyelnünk és meg tanulniuk a gyerekeknek. Talán ezért kellene még több figyelmet szentelni az energia nevezetésére, vagyis arra, hogy a gyerekek megértség az energia fogalmát és értelmét valamint, hogy különbséget tudjanak tenni a hétköznapi és a fizikában tanult megmaradó energia között. Persze mint az elején is említettem hat különböző energia fogalomról beszélhetünk. Ezekre is figyelni kell, hogy meg tudjuk őket különböztetni egymástól. Nehogy azt gondolják a diákok, hogy az az energia melyről a különböző bulvárlapokban olvasnak, az ugyanaz az energia, mint amiről fizikaórán tanulunk. Talán jót tenne, ha ezeket példákkal támasztanánk alá, és meg tudnánk mutatni, hogy ezek tényleg különböznek egymástól. De előbb csak a fizikai energiáról szeretnék beszélni, vagyis arról az energiáról, amit fizikaórán vezetünk be. Most csak egy olyan utat szeretnék bemutatni melljel talán egyszerűbb lesz bevezetni és megtanítani az energiát.

Ha már megtanítottuk a gyerekekkel az exergiát, ami a gyermeki energia fogalmunknak felel meg, akkor itt fel kell hívni a figyelmet arra, hogy ez nem egyezik meg azzal az energiával, amit most fogunk tanítani. Ez egy másik fogalom. Már tudják, hogy amit ők energiának neveztek eddig, az most az exergia, ez az amit a mindennapjainkban használunk, ez elfogy és újratermelődik. De amit most vezetünk be arra ez nem mondható.

Érdemes lenne kérdve kifejtős módon bevezetni az energiát, hisz a gyerekeknek is vannak némi tapasztalataik ezzel kapcsolatban, amit most elmondhat és különben is sokkal hatékonyabb a tanulás, ha ők maguk jönnek rá a lényegre. Célszerű lenne egyszerű hétköznapi példákból kiindulni, talán ők is mondhatnak példákat a saját tapasztalataik alapján, aztán ezeket megbeszélni.

Először a hő fogalmát vezetjük be:

Kalorimetria:

Most egy olyan egyszerű kísérletet szeretnék elmondani, amivel talán a gyerekek is könnyebben megértenék a különbséget a hő és a hőmérséklet között. Szerintem ezt egy fizikaórán elég egyszerűen meg lehetne valósítani. Ha mondjuk egy edényben, felforraljuk a vizet, és egy másik edénybe csapvizet teszünk. Majd vesszünk a forró vízből is bizonyos mennyiséget és a csapvízből is, majd mindkettőt külön-külön lemérjük, mondjuk egy mérőpohárba. Külön – külön megmérjük a hőmérsékletüket is, majd összeöntjük a két pohárban lévő vizet, és így is megmérjük a közös hőmérsékletüket. A mérést többször is elvégezhetjük különböző, mennyiségű vízzel és aztán következtetéseket vonhatunk le. Szerintem, ha az adatainkból egy táblázatot is készítünk, akkor már a gyerekek is rájönnek a lényegre.

Térfogat (ml)	Hőmérséklet ( ⁰ C)	Közös hőmérséklet ( ⁰ C)
200 50	59 26	52
200 50	25 59	32
100 100	72 32	52

6. Ábra

Itt a táblázatból is láthatjuk, hogy a közös hőmérséklet mindig annak a víznek a hőmérsékletéhez van közelebb, amelyikből több van. Ezt a gyerekek is észrevehetik és még több mérést is végezhetünk velük, hogy biztosak lehessünk a megállapításainkban. És, hogy tényleg láthassuk, hogy a közös hőmérséklet tulajdonképpen a mennyiségtől is függ.

Mivel itt azt vesszük észre, hogy beáll egy közös hőmérséklet, tehát valaminek történnie kell a vízben, hogy ez így kialakuljon, valaminek áramolnia kell, és erre mondhatjuk, hogy az a hő, ami áramlik és miatta változik meg a hőmérséklet.

Elég egyszerű kísérletekkel is meg lehet mutatni a különbségeket a diákoknak és még élvezni is fogják, ha egyedül végezhetik a kísérleteket. Ugyan ezt a kísérletet elvégezhetjük jéggel és forró vízzel is. Itt is megmérjük a jég és a víz tömegét külön – külön, a hőmérsékletüket is, majd összeöntés után is, mikor már a jég elolvadt. És még a jég látens hőjét is ki tudjuk számolni.

c_vm_k T_k= Lm + c_j m T_j

ebből

A hő-munka kapcsolat bevezetése.

A mindenki által jól ismert példa talán az lehet, hogy ha összedörzsöljük a kezünket, akkor az felmelegszik, munkavégzés hatására hőérzetünk megnő, vagy ha a kocsi lefékez, akkor kerekei felmelegszenek. Megkérhetjük, hogy mondjanak ők is példákat, és aztán megbeszéljük, hogy vajon miért is történik mindez. Persze a legjobb lenne, ha kísérletekkel is be tudnánk ezt mutatni. Azt mindenki külön megteheti, hogy összedörzsöli a kezét, aztán mit tapasztal. Vagy ha nézünk egy másik példát, a gyerekek tudják, hogy ha ég a lámpa, akkor ott hő is keletkezik, a fény mellett. Szóval elég sok olyan példát tudunk felhozni, amiről már a gyerekek is hallottak, elmondhatjuk, hogy azelőtt még nagyon régen hogyan gyújtottak tüzet.(de lehet, hogy már erről ők is tudnak valamit, akkor elmondják ők). Már akkor is a dörzsölést, azaz a súrlódást használták ki arra, hogy tüzet gyújtsanak. Addig dörzsölt egy száraz fadarabba vésett lyukat egy másik fadarabbal még tüzet nem kapott.

Ugyanezt megtehetjük differenciált csoportmunkában is, mondjuk, ha egyes csoportoknak más- más feladatot adunk elemzésre, vagy adhatjuk mindegyik csoportnak ugyanazt a feladatot, csak a lényeg, hogy először a csoportok, egymáskőzött, beszéljék meg a feladatot és utána közösen. Minden csoport mondja el a véleményét.

Itt például, feladhatjuk nekik csoportmunkában a kalorimetriánál emlegetett, feladatot, amit közösen kimérhetnek, és egyedül megmagyarázhatják a jelenséget.(de ez nem energia példa)

Szóval sorolhatnánk a példákat a mindennapi életből és a történelemből, de ezek után rákérdezhetünk, hogy mi a közös ezekben, a jelenségekben. Ha megvizsgáljuk, akkor azt látjuk, hogy mindig valami, itt konkrétan a mechanikai súrlódás alakul át hővé, tehát van egy mennyiség, ami a folyamat során végig megmarad. Ezt nevezzük energiának. Ez minden fizikai folyamatra jellemző. Van elektromos, helyzeti, mozgási, gravitációs és még folytathatnánk a sort, hogy milyen energiaforma létezik. Minden folyamat során ezek összege állandó, vagyis azok összege melyek éppen jelen vannak a folyamat során. Tehát itt kimondhatjuk, hogy az energia nem vész el csak átalakul egyik formájából a másikba.

Mielőtt még tovább lépnénk, elmesélhetjük azt a példát, amit Feynman mondott az energiával kapcsolatban. Képzeljünk el egy gyereket, akinek van 28 játékkockája, melyek törhetetlenek és feldarabolhatatlanok, és mind egyformák. A gyereket az anyukája reggel bezárja egy szobába a kockáival együtt és a nap végén, megszámolja a gyerek kockáit, és megdöbbenve tapasztalja, hogy a kockákból 28 van, bármit is tett a gyerek velük. Így ment ez egy pár napig, míg egyszer a nap végén azt tapasztalja, hogy csak 27 darab kocka maradt. De egy kicsit körbekutatva a lakást a mama megtalálja a 28.-ik kockát is, mivel biztos akar lenni abban, hogy a kockák száma nem változik. Aztán egy másik napon szintén kevesebb kocka maradt estére a szobában, a mama ismét mindent felkutatott, hogy megtalálja a kockákat, de sehol se voltak, míg nem észrevette, hogy nyitva az ablak és a két kocka kint hever a földön. Egy másik este viszont több kocka volt a szobában, ami szintén nem volt teljesen világos a mama számára, hogy az hogy kerülhetett oda. De utólag kiderült, hogy ott járt a szomszéd fiúcska, aki itt felejtett két kockát. Szóval a kockák eltűntek, majd előkerültek és néha még több is volt mind amennyi kellett. Egy nap azonban szintén eltűntek a kockák, ekkor a mama a sok keresés után már úgy döntött, hogy a dobozban fogja őket keresni, de a fiú nem engedte, hogy az anyukája kinyissa a dobozt. De mivel tudta, hogy mennyit nyom egy kocka és mikor üresen találta a dobozt, azt is lemérte, tehát így már ki tudta számolni, hogy mikor hiányzanak a kockák. Mivel tudta, hogy a doboz 16 unica, a kocka 3 unica, felírta az egyenletet:

( a látott kockák száma) + (( a doboz súlya) – 16 unica) /3 unica = állandó

Ha itt eltérés támadt, akkor tudta, hogy hiányzik valamennyi kocka, és ilyenkor az egyenletet újabb és újabb tagokkal bővítette ki. (Faymann 2000)

Most itt elmondhatjuk az energiamaegmaradást. Vajon miben hasonlít ez ahhoz? Az energiából is néha valamennyi kilép a rendszerből, mint a kockák mikor eltűntek, és néha valamennyi energia bekerül, mint a szomszéd gyerek kockái. De mindig megmarad, tehát valahol ott van, csak átalakult. Itt a megmaradásnál vigyázni kell, hogy nem adtunk-e valamit az energiához, vagy nem hagytuk-e el valamit. Az energiának több féle formája van, amivel szintén számolni kell és mindegyikhez más képlet, tartozik, ezekre is oda kell figyelni.

Igen itt talán elég nehéz elképzelni az energiát, elég absztrakt fogalom, nem mondhatjuk, hogy kis cseppekben, vagy csomagokban fordul elő, de viszont tudunk rá mondani egy számot, hogy most ez ennyi és ez nem változhat meg. Itt a példánkban tudtuk, hogy a kockák száma 28 és az nem változhat, ha akármit is tesz vele a gyerek. Tehát valahogy így kellene elképzelni az energiát, hisz máshoz nem nagyon tudjuk mihez hasonlítani, ez egy elég absztrakt fogalom a fizikában és talán elég nehezen emészthető is.

Ezek szerint van egy mennyiség mely minden folyamat során állandó. Ez az energiamegmaradás törvénye. Tudjuk, hogy a folyamatokban értéke állandó, és különböző megjelenési formái vannak. Az energia értékét már előttünk mások kimérték:

ez a mozgásnál az érték, ami a testnek Q= mcΔ T hőt ad át. Vagy a helyzeti energia.: E_helyzeti = mgh. Ezeket nehezen tudnánk lemérni az iskolában, ezért definíció szerint kell bevezetni. A bevezetésnél vigyázni kell arra, hogy a gyerekeknek ne csak ez az energiafajta maradjon meg a fejében, meg kell említeni, hogy többféle energia létezik. Azt is ki kell hangsúlyozni, hogy a hétköznapi energia fogalmunk nem egyezik meg azzal, amit a fizikaórán tanulunk. Más az energia, amit biológiaórán használunk és más az, amit földrajzórán. Vagyis a lényeges különbségekre fel kell hívni a figyelmüket, hogy könnyebben megértsék a fizikai energia fogalmát, és hogy különbséget tudjanak tenni az exergia és az energia között. A kettő nagyon hasonló, de mégsem ugyan az.

Befejezés

Összefoglalás

Most az energiát a termodinamikán keresztül vezetem be, mind nagyja része annak a tankönyveknek melyeket megvizsgáltam. Ezekben a gyerekek még nem tanulnak különböző képleteket és nem is nagyon foglalkoznak az energia bevezetésével. Talán, azért mert túl kevés az idő és elég sok az anyag, de szerintem akkor se kellene időt spórolni az energia bevezetésére, mert ez az egyik legtöbbet használt fogalmunk a mindennapi életben és a fizikában is. Ha ezt nem próbáljuk meg rendesen megtanítani a gyerekekkel, akkor lehet, hogy pont e miatt nem fogják érteni az egész fizikát, sőt akkor talán még nem is fogja őket érdekelni.

A dolgozatomban megpróbáltam felhívni a figyelmet arra, hogy az energia elég sok jelentéssel bír, és hogy ezek az energia fogalmak keverednek a gyerekek fejében. Fel soroltam azokat az energia fogalmakat, melyek különbözőek. Sokszor ezek a fogalmak keverednek a fejünkben és talán ezért is olyan nehezen értjük meg a fizikai energiát. Ugyanakkor nem csak az energiával, hanem annak megmaradásával is gond van, mert ugye a hétköznapi életünkben ezt nem tapasztaljuk. De remélem sikerült ezeket a fogalmakat egy kicsit szétválasztani és érthetőbbé tenni.

Azt is megnéztem, hogy egyes tankönyvek hogyan vezetik be az energiát, és ezeket összehasonlítottam. De itt nem csak az energiára korlátozódott a vizsgálatom, hanem az egész termodinamikára. Itt e tankönyvekben az energiát a hőtani részben vezetik be a tankönyvírók, kivéve a szerbiai tankönyveket. Az elemzések során aztán kitértem a hő és a hőmérséklet fogalmának bevezetésére is. Amit megfigyeltem, hogy nem nagyon különítik el a tankönyvírók e két fogalmat. De ezekre a dolgozatom során láthattunk példákat.

A tankönyvek összehasonlításának kidolgozásával, részt vettem egy nemzetközi konferencián, Tunéziában (Intrnational Meeting on Critical Analysis of School Science Textbooks) ahol szintén ilyen hasonló problémák vetődtek fel a tankönyvek kapcsán.

Valamint megpróbáltam felhívni a figyelmet arra is, hogy a hétköznapi és a fizikai energia nem ugyan az, és, hogy e kettő között különbséget tudjunk tenni, bemutattam, hogy hogyan lehetne bevezetni egy új fogalmat, amely a hétköznapi energiát tükrözné, ez az exergia. Megpróbáltam vázolni az exergia bevezetését az iskolában, hogy talán ha ezt is megtanulják a gyerekek akkor könnyebb lesz az energia fogalom megértése is. Persze az energia nem egy egyszerű fogalom, nem olyan könnyű bevezetni és megértetni a gyerekekkel, de megpróbáltam vázolni egy lehetőséget. Itt beleértettem mindjárt az energia-megmaradást is.

Zárszó

A dolgozatban bemutattam, hogy az energiának több jelentése van, de a legfontosabb, hogy a gyerekek keverik a hétköznapi energiát a fizikai energiával. Mivel az energia végig kísér bennünket fizika tanulmányainkon, ezért fontos, hogy megértsük. A tankönyvek összehasonlításában is a termodinamikai részt választottam, mert ott is nagyon sokszor megjelenik az energia, sőt abban a részben vezetik be. Itt jelenik meg először a belső energia fogalma is. A középiskolásoknál megjelennek a főtételek, és ott is szükség van az energia fogalmára, vagyis annak megértésére.

Remélem azért sikerült felhívni a figyelmet arra, hogy az energia oktatásával egy kis gondok vannak. Talán majd változik a helyzet a fizika oktatás terén is, persze itt nem csak az energia bevezetésének újragondolása a lényeg, de talán segíthet.

IRODALOMJEGYZÉK

Budó Ágoston ( 1997) : Kísérleti fizika I., Nemzeti Tankönyvkiadó, Budapest, 364-413

Csákány Antalné-Károlyházy Frigyes (2006): Fizika 7

Nemzeti Tankönyvkiadó, Budapest, 2. kiadás, 104-155

Egely György(2002): A leghasznosabb tudás

http://www.pointernet.pds.hu/ujsagok/evilag/2002/08/evilag-05.html

Energia

http://hu.wikipedia.org/wiki/Energia

G, Gamow ( 1965): A fizika története, Gondolat Kiadó, Budapest, 97-130

Gulyás János-Honyek Gyula-Markovits Tibor-Szalóki Dezső-Tomcsányi Péter-Varga Antal( 2003): Fizika 7

Műszaki Tankönyvkiadó, Budapest, 2. kiadás , 105-143

Javaslat a fizikai oktatásnak minimális követelményeire, Fizikai Szemle, 2004/1, 27 oldal

http://www.kfki.hu/fszemle/archivum/fsz0401/fizokt0401.html

Jovan P. Setrajcic-Darko V. Kapor : Fizika az általános iskolák 7. osztálya számára

Zavod za udzbenike i nastavna sredstva, Beograd

Karácsonyi Rezső(2003): Fizika a gimnáziumok 10. évfolyama számára, hőtan, elektromágnességtan ( humán érdeklődésű középiskolások számára)

Nemzeti Tankönyvkiadó, Budapest, 2003 2. kiadás, 3-85

Martinás Katalin: A közgazdaságtan újragondolása ( kézirat, 2007)

Martinás Katalin:: Aristotelian termodynamics, in: Martinás Katalin,L. Ropolyi, P. Szegedi ( eds.) (1991 /Thermodynamics: History and Philosophy - Facts, Trends, Debates/,

World Scientific, Singapore

Martinás Katalin ( 2003): Farkas Gyula élete és munkássága, ELFT, Budapest, 35-42

Martinás Katalin: Kelvini termodinamika

http://www.kfki.hu/~elftterm/kelvin.html

Martinás Katalin, Radnóti Katalin: Természetismeret oktatási programok, munkalapok http://www.ludens.elte.hu/~martinas/body/body.htm

Milan Raspopovic – Bojana Nikic-Dragisa Ivanovic – Jezdimir Tomic- Dragomir Krpic(2002):Fizika 7

Zavod za udzbenike i nastavna srestva, Beograd, 16. kiadás, 96-121

Milan Raspopovic – Svetozar Bozin- Emilo Danilovic( 1994): Fizika a 2. éves gimnazisták számára ( matematika irányzat)

Zavod za udzbenike i nastavna sredstva, Beograd , 7. kiadás, 1-84

Paál Tamás – Dr. Pászli István – Venczel Ottó( 2006): Fizika szakközépiskola 10. évfolyama

Nemzeti Tankönyvkiadó, Budapest, 3. kiadás, 134-204

Dr. Radnóti Katalin( 2002). A fizika tantárgy helyzete és fejlesztési feladatai, Új Pedagógiai Szemle, LII. Évfolyam, 5. szám 38-50 oldal

http://www.oki.hu/oldal.php?tipus=cikk&kod=tantargyak-Radnoti-Fizika

Radnóti Katalin(2005): Az önálló ismeretszerzésre alapozott tanítás lehetősége a természettudományi nevelésben, Új Pedagógiai Szemle, 10.szám 61-67 oldal

http://www.oki.hu/oldal.php?tipus=cikk&kod=2005-10-ta-Radnoti-Onallo

Radnóti Katalin, Nahalka István, Poór István, Wagner Éva ( 2002) : A fizikatanítás pedagógiája, Nemzeti Tankönyvkiadó, Budapest, 291-301

Radnóti Katalin: Fizikatanítás a középiskolában – a 2003-as obszervációs felmérés tapasztalatai

http://www.oki.hu/oldal.php?tipus=cikk&kod=kozepfoku-radnoti-fizikatanitas

Richard P. Feynman (2000) : Hat könnyed előadás, Park Könyvkiadó – Akkord Könyvkiadó, Budapest, 89-106

R. P. Feynman, R.B. Leighton, M. Sands ( 1969): Mai fizika, Műszaki könyvkiadó, Budapest, 65-84

Szabó Árpád, Szabó Timea (2003): A fizika története, Akadémiai Kiadó, Budapest, 133-150

Tisza László ( 1992): A termodinamika megalapozása, Fizikai Szemle, 8. szám 285 oldal

http://www.kfki.hu/fszemle/archivum/fsz9208/tisza9208.html

Vantsó Erzsébet( 2000): Gondolatok, dilemmák, javaslatok a fizika tantervben

http://www.oki.hu/oldal.php?tipus=cikk&kod=esely-Vantso-Gondolatok

Zátonyi Sándor (2006): Fizika az általános iskolák 7. osztálya számára

Nemzeti Tankönyvkiadó, Budapest, 3. kiadás, 135-192

http://hps.elte.hu/~szegedi/tudtort/vb3/page_01.htm kép ( pupin)

Ábra jegyzék

1. Ábra: Fizikatanárok véleménye a tankönyv választékról………………….

2. Ábra:……………………………………………………………………….

3. Ábra…………………………………………………………………………..

4.Ábra……………………………………………………………………………..

5.Ábra…………………………………………………………………………….

6. Ábra……………………………………………………………………………….

7. Ábra………………………………………………………………………………..

Függelék

KW_EN	KW_HU	KW_SR	KW_PL	TB_HU_L_1	TB_HU_L_2	TB_HU_L_3	TB_PL_L_2	TB_PL_L_3
Thermal physics
Pressure	Nyomás	Pritisak	Ciśnienie	78
Mass	Tömeg	Masa	Masa	27	38	48		3015
Liquids	Folyadék	Tečnost	Ciecze	82		106	1130	3009
Solid body	Szilárd test	Cvrsto telo	Ciało stałe	120		139	1124
Metal	Fém	Metal	Metal	141	119	143	1124
Non-metals	Nem fém	Ne metal	Niemetal	141	121	143	1128
Combustible	Fűtőanyag	Gorivo	Paliwo		122
Temperature	Hőmérséklet	Temperatura	Temperatura	104	106	135	1133
Thermometer	Hőmérő	Termometar	Termometr	104	106	135	1137
Celsius skale	Celsius skála	Celsius skala	Skala Celsjusza	104	106	135		3105
Kelvin skale	Kelvin skála	Kelvin skala	Skala Kelvina					3105
Warming	Melegítés	Zagrevanje	Ogrzewanie	104	107
Cooling	Hűtés	Hladjenje	Chłodzenie	104	107
Heat conduction	Hővezetés	Priovođenje	Przewodnictwo cieplne	104	119	142
Thermic interaction	Termikus kölcsönhatás	Termicka interakcija	Oddziaływanie cieplne	104		153
Thermodynamic basic terms	Hőtani alapfogalmak	Termicki temelji	Podstawowe pojęcia termodynamiczne		106
Heat phenomena	Hőjelenség	Toplotne pojave	Zjawiska cieplne
Combustion	Égés	Gorenje	Spalanie				1070
matter	Anyag	Materija	Materia				1130	3008
states of matter	Anyagállapotok	Materijalna stanja	Stany materii				1130	3009
Diffusion	Diffúzió	Difuzija	Dyfuzja					3011
Tyndall-phenomena	Tyndall-jelenség	Tyndall effekat	Zjawisko Tyndalla
Substance	Szubsztancia	Substanca	Substancja
Energy
Energy	Energia	Energija	Energia	106	107	147	1025
Energy carriers	Energiahordozók	Nosaci energije	Nośniki energii	106
Work	Munkavégzés	Vrsenjem rada	Wykonywanie pracy	107	131	147
Energy source	Energiaforrás	Izvor energije	Źródło energii	108	122
Conservation of energy	Energiamegmaradás	Odrzavanje energije	Zachowanie energii	108
Energy changing	Energiaváltozások	Promena energije	Przemiany energii		116	148
Thermal energy	Termikus energia	Termicka energija	Energia cieplna	108		176	1070
Chemical energy	Kémiai energia	Hemijska energija	Energia chemiczna	108				3092
Internal energy	Belső energia	Unutrašnja energija	Energia wewnętrzna	109	114			3093
Mechanical energy	Mechanikai energia	Mehanička energija	Energia mechaniczna	144	132	176
Kinetic energy	Kinetikus energia	Kinetička energija	Energia kinetyczna	144	133	175		3092
Potential energy	Helyzeti energia	Potencialna energija	Energia potencjalna	146	133			3092
Elastic energy	Rugalmas energia	Elastična energija	Energia elastyczna	147	133	176
Gravitational energy	Gravitációs energia	Gravitaciona energija	Energia grawitacyjna	147
Electrostatic energy	Elektrosztatikus energia	Elektrostaticna energija	Energia elektrostatyczna				1070
Nuclear energy	Nukleáris energia	Nuklearna energija	Energia jądrowa
Energy kinds	Energia fajták	Vrste energije	Rodzaje energii			175		3092
Height energy	Magassági energia	Visinska energija	(not appears in Polish)			176
Energy transformation	Energiaátadás	Transformacija energije	Transformacje energii					3093
Work
Work	Munka	Rad	Praca	148
Mechanical work	Mechanikai munka	Mehanički rad	Praca mechaniczna	148
Joule [unit]	Joule	Joule	Joule	107	115	147		3093
Power	Teljesítmény	Moc	Moc	149	139	187
Volume work	Térfogati munka	Zapreminski rad	Praca objętościowa
Energy release in chemical reaction	Energia felszabadulása a kémiai reakcióban	Oslobadjanje energije u hemijskim procesima	Wydzielanie energii w reakcjach chemicznych					3019
Mass conservation	Tömeg megmaradás	Odrzavanje masa	Zachowanie masy					3019
Calorimetry
Heat of combustion	Égéshő		Ciepło spalania	109	122	150
Specific heat	Fajhő	Specifična toplota	Ciepło właściwe	111	116	157
Lamp	Borszeszégő	Lampa	Palnik spirytusowy	111
Heat
Heat	Hő	Količina toplote	Ciepło	113	107	147
Heat transfer	Hőátadás	Toplotna razmena	Przekaz ciepła	113	119
Heat-removal	Hőelvonás	Uzimanje toplote	Odprowadzenie ciepła	113
Particles	Részecske	Čestica	Cząstka	114		161
Gas	Gáz	Gas	Gaz	118		141	1130	3009
Heat motion	Hő mozgás	Kretanje toplote	Ruch cieplny	119
Thermal expansion	Hőtágulás	Širenje pri zagrevanju	Rozszerzalnośc cieplna	120	108	139
Bimetal	Bimetál	Bimetal	Bimetal	122	110
Heat capacity	Hőkapacitás	Toplotni kapacitet	Pojemnośc cieplna
Heat insulator	Hőszigetelő	Termoizolacioni material	Izolator cieplny	141	119	143		3103
Heat convection	Hőáramlás	Strujanje	Konwekcja cieplna	142	119	143		3103
Heat radiation	Hősugárzás	Zračenje	Promieniowanie cieplne	142	120	144		3103
Heat expansion coefficient	Hőtágulási együttható	Koeficijent toplotnog sirenja	Współczynnik rozszerzalności cieplnej		109
Change of state	Halmazállapotváltozás	Promena agregatnog stanja	Zmiana stanu		124
Heat absorption	Hőfelvétel	Absorpcija toplote	Absorpcja ciepła		125
Heat rejection	Hőleadás		(not used in Polish)		125			3105
Boltzmann-constant	Boltzmann-állandó	Bolcmanova konstanta	Stała Boltzmanna
Free path	Szabad úthossz	Duzina slobodnog puta	Droga swobodna
Heat stretch	Hőterjedés	Sirenje toplote	Rozchodzenie się ciepła			142
Triple point	Harmat pont	Trojna tacka	Punkt potrójny
Heat condition	Hőállapot	Toplotna stanja	(not used in Polish)					3103
Heat conductors	Hő vezető	Nosac	Przewodniki ciepła					3103
Heat balance	Hőegyenleg	Toplotni bilans	Bilans cieplny
Steam engine	Gőzgép	Parna mašina	Maszyna parowa	151	133	182
Heat engines	Hőerőgépek	Toplotni motori	maszyny cieplne	152	136	182		3148
Steam-locomotive	Gőzmozdony	Parna lokomotiva	Lokomotywa parowa	153	133
Turbine	Gőzturbina	Turbina	Turbina	153		182
Piston	Dugattyú	Klip	Tłok	154	133	182
Phase transtions
Phase transformation	Fázisátalakulások	Fazni prelazi	Przemiana fazowa
Melting	Olvadás	Topljenje	Topnienie	126	124	163	1132
Melting point	Olvadáspont	Temperatura topljenja	Temperatura topnienia	127	124	164
Heat fusion	Olvadáshő	Specificnu toplotu topljenja	Ciepło topnienia	127	124	165
Freezing	Fagyás	Očvršćavanje	Zamarzanie	130	124	164	1132
Freezing point	Fagyáspont	Temperatura očvršćavanja	Temperatura zamarzania	131	124	166
Freezing heat	Fagyáshő	Toplota ocvrscavanja	Ciepło zamarzania	131		166
Evaporation heat	Párolgáshő	Toplota isparavanja	Ciepło parowania
Evaporation	Párolgás	Isparavanje	Parowanie	132	128	168	1133
Gaseous	Légnemű		Gazowy	132	129
Boiling	Forrás	Ključanje	Wrzenie	135	126	171	1132
Condensation	Lecsapódás	Kondenzacija	Kondensacja	135	126	173	1133
Boiling point	Forráspont	Temperatura ključanja	Temperatura wrzenia	136	126	171
Boiling heat	Forráshő	Toplota kljucanja	Ciepło wrzenia	136	127	172
Sublimation	Szublimáció	Sublimacija	Sublimacja			170
Condensation	Kondenzáció	Kondenzacija	Kondensacja
Condensation heat	Kondenzációs hő	Toplota kondenzacije	Ciepło kondensacji
Triplet point	Hármaspont	Trojna tačka	Punkt potrójny
Steaming	Gőzölgés	Isparavanje	???
Ideal gas
Ideal gas	Ideális gáz	Idealni gas	Gaz doskonały
Isotherm	Izoterm	Izotermski	Izoterma
Isochors	Isochor	Izohorski	Izochora
Isobar	Izobár	Izobarski	Izobara
Clapeyron equation	Klapejron egyenlet	Klapejronova jednacina	Równanie Clapeyrona
State variable	Állapotjelző	Thermodynamic parametri	Zmienna stanu
Molar heat	Mólhő	Molarni toplotni kapacitet	Ciepło molowe
The first law of thermodynamics	Termodinamika első főtétele	Prvi zakon termodinamike	Pierwsza zasada termodynamiki
Amount of material	Anyagmennyiség	Kolicina materijala	Ilośc materiału
Volume	Térfogat	Zapremina	Objętośc
Changes of state	Állapotváltozások	Menjanje stanja	Zmiana stanu
Equation of state	Állapotegyenlet	Jednacina stanja	Równanie stanu
Molar mass	Moláris tömeg	Molarna masa	Masa molowa
Avogadro-number	Avogadro-szám	Avogadrova konstanta	Liczba Avogadry
Conducted gas low	Egyesített gáztörvény		????????
Universal gas constant	Univerzális gázállandó	Univerzalna gasna konstanta	Stała gazowa
Real gas	Reális gáz	Realni gas	Gaz rzeczywisty
The second law of thermodynamics
The second law of thermodynamics	Termodinamika második főtétele	Drugi zakon termodinamike	Druga zasada termodynamiki
Adiabatic process	Adiabatikus folyamat	Adiabatski proces	Proces adiabatyczny
Quasi-static process	Kvázisztatikus folyamat	Kvázistaticki proces	Proces kwazystatyczny
Reversible process	Reverzibilis folyamat	Reverzibilni proces	Proces odwracalny
Irreversible process	Irreverzibilis folyamat	Ireverzibilni proces	Proces nieodwracalny
Entropy	Entrópia	Entropija	Entropia
Carnot-cycle	Carnot-féle körfolyamat	Karnoov ciklus	Cykl Carnota
Perpetuum mobile	Perpetuum mobile	Perpetuum mobile	Perpetuum mobile
Process	Folyamat	Proces	Proces
Efficiency	Hatásfok	Koeficijent korisnog dejstva	Sprawnośc	151	141	193
Statistical physics
Atoms	Atomok	Atomi	Atom				1130	3010
Molecule	Molekulák	Molekule	Cząsteczka					3010
Atomic mass	Atomtömeg	Masa atoma	masa atomowa
Mass unit	Tömegegység	Masovna jedinica	Jednostka masy
Hydrostatic pressure	Hidrosztatikai nyomás	Hidrostaticki pritisak	Ciśnienie hydrostatyczne
Weight ratio laws	Súlyviszonytörvények		Prawa stosunków masy
Brown-motion	Brown-mozgás	Kretanje-Brown	Ruchy Browna
Kinetic theory of gases	Kinetikus gázelmélet	Kineticka teorija gasa	Kinetyczna teoria gazów
Equilibrium process	Egyensúlyi folyamatok	Proces ravnoteze	Proces równowagowy
Le Chatelier-Brown-theory	Le Chatelier-Brown-elv	Teorija le Chatelier-Browna	Zasada le Chateliera-Browna
Theorem of the equipartition of energy	Ekvipartíció elve	Teorija ekviparticije	Zasada ekwopartycji energii
Elementary particles
Proton	Proton	Protoni	Proton
Neutron	Neutron	Neutroni	Neutron
Electron	Elektron	Elektroni	Elektron
Elementary electric quantity of charge	Elemi elektromos töltésmennyiség	Elementarna koločina naelektrisanja	Elementarny ładunek elektryczny
Ion	Ion	Ioni	Jon
Photons	Fotonok	Fotoni	Fotony
Other terms
Crystalline	Kristályos	Kristalni	Krystaliczny
Amorphous	Amorf	Amorfni	Amorficzny
Cohesion force	Kohéziós erők	Sila kohezije	Siła kohezji
Chemical transformation	Kémiai átalakulások	Hemijska transformacija	Przemiana chemiczna					3018
KW_EN	KW_HU	KW_SR	KW_PL	TB_HU_U-1	TB_HU_U_2	TB_SR_U_1	TB_SR_1	TB_SR_2
Thermal physics
Pressure	Nyomás	Pritisak	Ciśnienie	21	142	10
Mass	Tömeg	Masa	Masa				12
Liquids	Folyadék	Tečnost	Ciecze				106
Solid body	Szilárd test	Cvrsto telo	Ciało stałe				106
Metal	Fém	Metal	Metal					82
Non-metals	Nem fém	Ne metal	Niemetal					82
Combustible	Fűtőanyag	Gorivo	Paliwo
Temperature	Hőmérséklet	Temperatura	Temperatura	3	140	12	100	75
Thermometer	Hőmérő	Termometar	Termometr	13	140		102	78
Celsius skale	Celsius skála	Celsius skala	Skala Celsjusza					77
Kelvin skale	Kelvin skála	Kelvin skala	Skala Kelvina					77
Warming	Melegités	Zagrevanje	Ogrzewanie				98
Cooling	Hűtés	Hladjenje	Chłodzenie				98
Heat conduction	Hővezetés	Priovođenje	Przewodnictwo cieplne				108	82
Thermic interaction	Termikus kölcsönhatás	Termicka interakcija	Oddziaływanie cieplne		169
Thermodynamic basic terms	Hőtani alapfogalmak	Termicki temelji	Podstawowe pojęcia termodynamiczne	3	139
Heat phenomena	Hőjelenség	Toplotne pojave	Zjawiska cieplne				98	75
Combustion	Égés	Gorenje	Spalanie
matter	Anyag	Materija	Materia
states of matter	Anyagállapotok	Materijalna stanja	Stany materii
Diffusion	Diffúzió	Difuzija	Dyfuzja		136	7
Tyndall-phenomena	Tyndall-jelenség	Tyndall effekat	Zjawisko Tyndalla		136
Substance	Szubsztancia	Substanca	Substancja					86
Energy
Energy	Energia	Energija	Energia
Energy carriers	Energiahordozók	Nosaci energije	Nośniki energii
Work	Munkavégzés	Vrsenjem rada	Wykonywanie pracy	52	171	22
Energy source	Energiaforrás	Izvor energije	Źródło energii
Conservation of energy	Energiamegmaradás	Odrzavanje energije	Zachowanie energii
Energy changing	Energiaváltozások	Promena energije	Przemiany energii
Thermal energy	Termikus energia	Termicka energija	Energia cieplna
Chemical energy	Kémiai energia	Hemijska energija	Energia chemiczna
Internal energy	Belső energia	Unutrašnja energija	Energia wewnętrzna	52	153	21	99	75
Mechanical energy	Mechanikai energia	Mehanička energija	Energia mechaniczna
Kinetic energy	Kinetikus energia	Kinetička energija	Energia kinetyczna	52	146	5		75
Potential energy	Helyzeti energia	Potencialna energija	Energia potencjalna	52				75
Elastic energy	Rugalmas energia	Elastična energija	Energia elastyczna
Gravitational energy	Gravitációs energia	Gravitaciona energija	Energia grawitacyjna
Electrostatic energy	Elektrosztatikus energia	Elektrostaticna energija	Energia elektrostatyczna
Nuclear energy	Nukleáris energia	Nuklearna energija	Energia jądrowa
Energy kinds	Energia fajták	Vrste energije	Rodzaje energii
Height energy	Magasági energia	Visinska energija	(not appears in Polish)
Energy transformation	Energiaátadás	Transformacija energije	Transformacje energii
Work
Work	Munka	Rad	Praca
Mechanical work	Mechanikai munka	Mehanički rad	Praca mechaniczna
Joule [unit]	Joule	Joule	Joule
Power	Telyesitmény	Moc	Moc
Volume work	Térfogati munka	Zapreminski rad	Praca objętościowa	74
Energy release in chemical reaction	Energia felszabadulása a kémiai reakcióban	Oslobadjanje energije u hemijskim procesima	Wydzielanie energii w reakcjach chemicznych
Mass conservation	Tömeg megmaradás	Odrzavanje masa	Zachowanie masy
Calorimetry
Heat of combustion	Égéshő		Ciepło spalania			25
Specific heat	Fajhő	Specifična toplota	Ciepło właściwe	54	175	25	104	85
Lamp	Borszeszégő	Lampa	Palnik spirytusowy	6
Heat
Heat	Hő	Količina toplote	Ciepło	4	170	24	98	75
Heat transfer	Höátadás	Toplotna razmena	Przekaz ciepła					81
Heat-removal	Hőelvonás	Uzimanje toplote	Odprowadzenie ciepła	55
Particles	Részecske	Čestica	Cząstka	58	135		98
Gas	Gáz	Gas	Gaz
Heat motion	Hőmozgás	Kretanje toplote	Ruch cieplny				98
Thermal expansion	Hőtágulás	Širenje pri zagrevanju	Rozszerzalnośc cieplna	5			103	80
Bimetal	Bimetál	Bimetal	Bimetal
Heat capacity	Hőkapacitás	Toplotni kapacitet	Pojemnośc cieplna		175
Heat insulator	Hőszigetelő	Termoizolacioni material	Izolator cieplny
Heat convection	Hőáramlás	Strujanje	Konwekcja cieplna				108	82
Heat radiation	Hősugárzás	Zračenje	Promieniowanie cieplne				108	84
Heat expansion coefficient	Hőtágulási együttható	Koeficijent toplotnog sirenja	Współczynnik rozszerzalności cieplnej	5
Change of state	Halmazállapotváltozás	Promena agregatnog stanja	Zmiana stanu	55
Heat absorption	Hőfelvétel	Absorpcija toplote	Absorpcja ciepła	55
Heat rejection	Hőleadás		(not used in Polish)
Boltzmann-constant	Boltzmann-állandó	Bolcmanova konstanta	Stała Boltzmanna	64	177	4
Free path	Szabad úthossz	Duzina slobodnog puta	Droga swobodna			5
Heat stretch	Hőterjedés	Sirenje toplote	Rozchodzenie się ciepła				108
Triple point	Harmatpont	Trojna tacka	Punkt potrójny				107
Heat condition	Hőállapot	Toplotna stanja	(not used in Polish)	3
Heat conductors	Hő vezető	Nosac	Przewodniki ciepła
Heat balance	Hőegyenleg	Toplotni bilans	Bilans cieplny					86
Steam engine	Gőzgép	Parna mašina	Maszyna parowa
Heat engines	Hőerőgépek	Toplotni motori	maszyny cieplne		182
Steam-locomotive	Gőzmozdony	Parna lokomotiva	Lokomotywa parowa
Turbine	Gőzturbina	Turbina	Turbina
Piston	Dugattyú	Klip	Tłok
Phase transtions
Phase transformation	Fázisátalakulások	Fazni prelazi	Przemiana fazowa				106	88
Melting	Olvadás	Topljenje	Topnienie	85			106	89
Melting point	Olvadáspont	Temperatura topljenja	Temperatura topnienia	86			107	90
Heat fusion	Olvadáshő	Specificnu toplotu topljenja	Ciepło topnienia	85				90
Freezing	Fagyás	Očvršćavanje	Zamarzanie	85			106	89
Freezing point	Fagyáspont	Temperatura očvršćavanja	Temperatura zamarzania	87			107	90
Freezing heat	Fagyáshő	Toplota ocvrscavanja	Ciepło zamarzania
Evaporation heat	Párolgáshő	Toplota isparavanja	Ciepło parowania	90
Evaporation	Párolgás	Isparavanje	Parowanie	87			107	91
Gaseous	Légnemü		Gazowy				106
Boiling	Forrás	Ključanje	Wrzenie	90			107	93
Condensation	Lecsapódás	Kondenzacija	Kondensacja				107
Boiling point	Forráspont	Temperatura ključanja	Temperatura wrzenia				107	93
Boiling heat	Forráshő	Toplota kljucanja	Ciepło wrzenia
Sublimation	Szublimáció	Sublimacija	Sublimacja	92			108	91
Condensation	Kondenzácio	Kondenzacija	Kondensacja	92				92
Condensation heat	Kondenzációs hő	Toplota kondenzacije	Ciepło kondensacji	94
Triplet point	Hármaspont	Trojna tačka	Punkt potrójny					94
Steaming	Gőzölgés	Isparavanje	???				107
Ideal gas
Ideal gas	Ideális gáz	Idealni gas	Gaz doskonały	46		9
Isotherm	Izoterm	Izotermski	Izoterma	36	158	12
Isochors	Isochor	Izohorski	Izochora	32	161	14
Isobar	Izobár	Izobarski	Izobara	31	160	16
Clapeyron equation	Klapejron egyenlet	Klapejronova jednacina	Równanie Clapeyrona			18
State variable	Állapotjelző	Thermodynamic parametri	Zmienna stanu	19		20
Molar heat	Mólhő	Molarni toplotni kapacitet	Ciepło molowe		175	26
The first law of thermodynamics	Termodinamika első főtétele	Prvi zakon termodinamike	Pierwsza zasada termodynamiki	72	179	27
Amount of material	Anyagmennyiség	Kolicina materijala	Ilośc materiału	19	152
Volume	Térfogat	Zapremina	Objętośc	21	140
Changes of state	Állapotváltozások	Menjanje stanja	Zmiana stanu		156
Equation of state	Állapotegyenlet	Jednacina stanja	Równanie stanu		165
Molar mass	Moláris tömeg	Molarna masa	Masa molowa	20	152
Avogadro-number	Avogadro-szám	Avogadrova konstanta	Liczba Avogadry	69
Conducted gas low	Egyesített gáztörvény			43
Universal gas constant	Univerzális gázállandó	Univerzalna gasna konstanta	Stała gazowa	44
Real gas	Reális gáz	Realni gas	Gaz rzeczywisty		174
The second law of thermodynamics
The second law of thermodynamics	Termodinamika második főtétele	Drugi zakon termodinamike	Druga zasada termodynamiki	78	180	27
Adiabatic process	Adiabatikus folyamat	Adiabatski proces	Proces adiabatyczny	77	171	33
Quasi-static process	Kvázisztatikus folyamat	Kvázistaticki proces	Proces kwazystatyczny			36
Reversible process	Reverzibilis folyamat	Reverzibilni proces	Proces odwracalny	82		38
Irreversible process	Irreverzibilis folyamat	Ireverzibilni proces	Proces nieodwracalny	82		39
Entropy	Entrópia	Entropija	Entropia			42
Carnot-cycle	Carnot-féle körfolyamat	Karnoov ciklus	Cykl Carnota	84		51
Perpetuum mobile	Perpetuum mobile	Perpetuum mobile	Perpetuum mobile		181
Process	Folyamat	Proces	Proces	19
Efficiency	Hatásfok	Koeficijent korisnog dejstva	Sprawnośc			52
Statistical physics
Atoms	Atomok	Atomi	Atom
Molecule	Molekulák	Molekule	Cząsteczka
Atomic mass	Atomtömeg	Masa atoma	masa atomowa	20
Mass unit	Tömegegység	Masovna jedinica	Jednostka masy	20
Hydrostatic pressure	Hidrosztatikai nyomás	Hidrostaticki pritisak	Ciśnienie hydrostatyczne	24
Weight ratio laws	Súlyviszonytörvények		Prawa stosunków masy	49
Brown-motion	Brown-mozgás	Kretanje-Brown	Ruchy Browna	58
Kinetic theory of gases	Kinetikus gázelmélet	Kineticka teorija gasa	Kinetyczna teoria gazów	61
Equilibrium process	Egyensúlyi folyamatok	Proces ravnoteze	Proces równowagowy	76
Le Chatelier-Brown-theory	Le Chatelier-Brown-elv	Teorija le Chatelier-Browna	Zasada le Chateliera-Browna	86
Theorem of the equipartition of energy	Ekvipartíció elve	Teorija ekviparticije	Zasada ekwopartycji energii	69	177
Elementary particles
Proton	Proton	Protoni	Proton					74
Neutron	Neutron	Neutroni	Neutron					74
Electron	Elektron	Elektroni	Elektron					74
Elementary electric quantity of charge	Elemi elektromos töltésmennyiség	Elementarna koločina naelektrisanja	Elementarny ładunek elektryczny					74
Ion	Ion	Ioni	Jon					74
Photons	Fotonok	Fotoni	Fotony					84
Other terms
Crystalline	Kristályos	Kristalni	Krystaliczny					88
Amorphous	Amorf	Amorfni	Amorficzny					88
Cohesion force	Kohéziós erők	Sila kohezije	Siła kohezji				106
Chemical transformation	Kémiai átalakulások	Hemijska transformacija	Przemiana chemiczna